126. For the network shown in the given figure, voltage V_B will be
     
     

1. 1. (j 5.33) V

   
   
   

   2. (5.33) V

   
   
   

   3. (– j 5.33) V

   
   
   

   4. (j 3.33) V

   
   
   

---

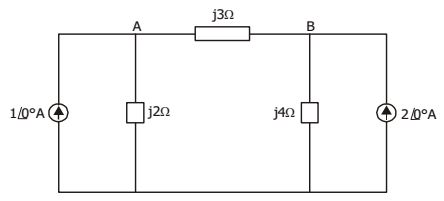
1. View Hint View Answer Discuss in Forum

   Drawing equivalent circuit, we have
   
   

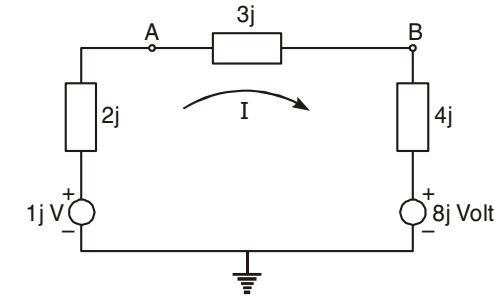
   Current , I =	8j - 2j	=		-	2		amp
   	9j				3

   
   Then, V_B = 8j + 4j.I
   

   = 8j -	8j
   	3

   
   

   =	16j	= 5.33j V
   	3

   
   

   Correct Option: A

   Drawing equivalent circuit, we have
   
   

   Current , I =	8j - 2j	=		-	2		amp
   	9j				3

   
   Then, V_B = 8j + 4j.I
   

   = 8j -	8j
   	3

   
   

   =	16j	= 5.33j V
   	3

   
   

---

127. In the network shown in the given figure, which of the following equations would represent the equation for loop 3?
     
     

1. 1. – I₁ + 4 I₂ + 11 I₃ = 0

   
   
   

   2. I₁ + 4 I₂ + 11 I₃ = 0

   
   
   

   3. – I₁ - 4 I₂ + 11 I₃ = 0

   
   
   

   4. I₁ + 4 I₂ + 6 I₃ = 0

   
   
   

---

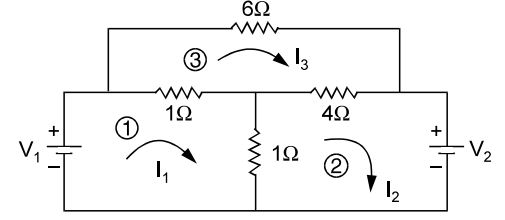
1. View Hint View Answer Discuss in Forum

   Loop equation is
   (I ₃ – I₁) 1 + 6 I₃ + (I₃ – I₂). 4 = 0
   ∴ – I₁ – 4 I₂ + 11 I₃ = 0

   Correct Option: C

   Loop equation is
   (I ₃ – I₁) 1 + 6 I₃ + (I₃ – I₂). 4 = 0
   ∴ – I₁ – 4 I₂ + 11 I₃ = 0

---

---

128. Thevenin equivalent of the network shown in Fig. (a) is 10 V in series with a resistance of 2 Ω. If a resistance of 3 Ω is connected across AB as shown in Fig. (b), then Thevenin equivalent of the modified network across AB will be
     
     
     

1. 1. 10 V in series with 1.2 Ω resistance

   
   
   

   2. 6 V in series with 1.2 Ω resistance

   
   
   

   3. 10 V in series with 5 Ω resistance

   
   
   

   4. 6 V in series with 5 Ω resistance

   
   
   

---

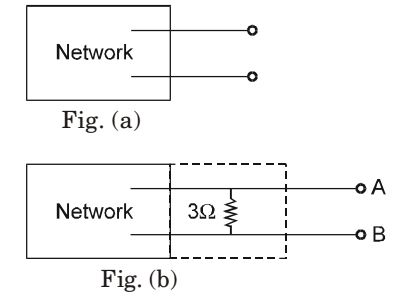
1. View Hint View Answer Discuss in Forum

   Req =	2 × 3	= 1.2 Ω
   	2 + 3

   
   

   Voc =	10 × 3	= 6 V
   	3 + 2

   Correct Option: B

   Req =	2 × 3	= 1.2 Ω
   	2 + 3

   
   

   Voc =	10 × 3	= 6 V
   	3 + 2

---

129. Norton’s equivalent of circuit shown in Fig.(a) is drawn in the circuit shown in Fig.(b). The values of ISC and Req in Fig.(b) are respectively
     
     

1. 1. 	5	A and 2 Ω
      	2

      
      

   
   
   

   2. 	2	A and 3 Ω
      	5

      
      

   
   
   

   3. 	4	A and	12	Ω
      	5		5

      
      

   
   
   

   4. 	2	A and 2 Ω
      	5

      
      

   
   
   

---

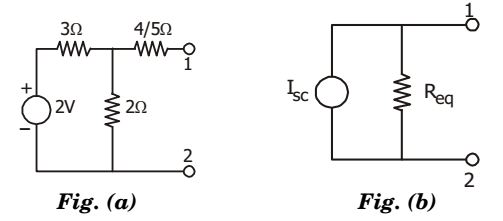
1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: D

   NA

---

---

130. The state equation for the current I₁ shown in the network given below in terms of the voltage V_x and the independent source V, is given by
     

1. 1. 	dI1	= -1.4Vx - 3.75I1 +	5	V
      	dt		4

   
   
   

   2. 	dI1	= -1.4Vx - 3.75I1 -	5	V
      	dt		4

   
   
   

   3. 	dI1	= -1.4Vx + 3.75I1 +	5	V
      	dt		4

   
   
   

   4. 	dI1	= -1.4Vx + 3.75I1 -	5	V
      	dt		4

      
      

   
   
   

---

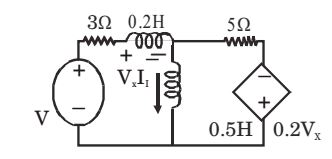
1. View Hint View Answer Discuss in Forum

   
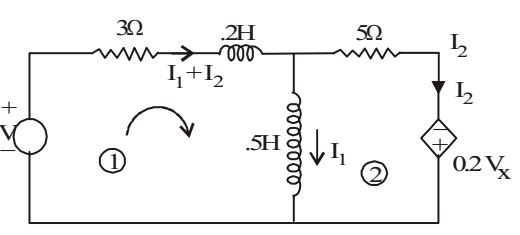
   Using KVL in loop (1), we get
   

   V = 3(I1 + I2) + Vx + 0.5	dI1	........(1)
   	dt

   
   and using KVL in loop (2), we have
   

   and 0.5	dI1	= 5I2 - 0.2Vx .......(2)
   	dt

   
   Solving (1) and (2),
   

   	dI1	=	5	V -	15	I1 - 1.4Vx
   	dt		4		4

   
   

   Correct Option: A

   
   Using KVL in loop (1), we get
   

   V = 3(I1 + I2) + Vx + 0.5	dI1	........(1)
   	dt

   
   and using KVL in loop (2), we have
   

   and 0.5	dI1	= 5I2 - 0.2Vx .......(2)
   	dt

   
   Solving (1) and (2),
   

   	dI1	=	5	V -	15	I1 - 1.4Vx
   	dt		4		4

   
   

---