Electric circuits miscellaneous
- Three capacitors C1, C2, and C3, whose values are 10μF, 5μF, and. 2μF respectively, have breakdown voltages of 10V, 5V, and 2V respectively. For the i nt er connect i on shown, t he maxi mum safe voltage in Volts that can be applied across the combination and the corresponding total charge in μC stored in the effective capacitance across the terminals are respectively
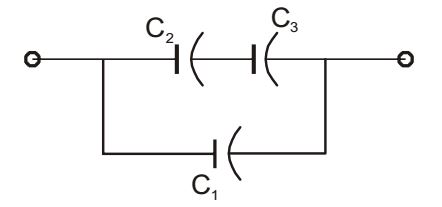
-
View Hint View Answer Discuss in Forum
Given values :
Capacitance Value Voltage Breakdown C1 10 F 10V C2 5 F 5V C3 2 F 2V
Given circuit :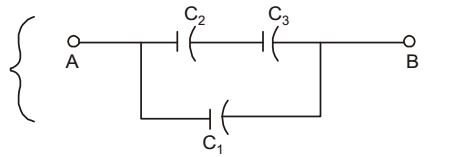
To find :
Max. safe voltage in volts that can be applied across the combination and Corresponding total charge is C.
Devising a plan :
(a) We will first calculate equivalent capacitance of given figure.
(b) By calculating capacitance, we can check which answer can be the solution, it reduce your effort in solving problem.
(c) Then apply the remaining answer for remaining options.
Solving :
Equivalent capacitance, as C2 & C3 are in series and we know that when capacitanceare in series equivalent capacitance = C2 C3 C2 + C3
& when two capacitor ar e in parallel then their addition= C1 + C2 C3 C2 + C3 * C = C1 + C2 C3 = 10μF + 5μF × 2μF = 11.4285 F C2 + C3 5μF + 2μF
Now check the option by using formula CV = θ
(a) 2.8 × 11.4285 = 32 μC ≠ 36 μC (option (a) is wrong)
hence ‘c’ option can be right
Now when 7V
(b) 7V × 11.4285 F = 80 c ≠ 119 C {B is hence ‘d’ option is right. only ‘c’ & ‘d’ are left.
⇒ Now apply 7V first in given circuit,
when voltage across AB is 7V then C1 can handle it broz max breakdown voltage across is 10Y.
and across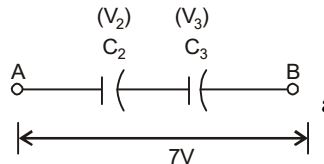
as they are in series so charge across them will be same.
Q2 = Q3
C2 V2 = C3 V3
C2 V2 = C3 V3 [V2 + V3 = 7V]
C2 V2 = C3 (7 – V2)
C2 V2 = 7C3 – C3 V2V2 = 7 C3 C2 + C3 V2 = 7 × 2 = 2 V 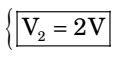
2 + 5
and V3 = 7 – V2 = 7 – 2V3 = 5 V
As when we take ‘7V’ then for that V2 = 2V & V3 = 5V, but max voltage across V3can be 2V [because above which it breakdown].
asV3 ≤ 2 V
But, when we take 7V then V3 have to be 5V which is not possible hence ‘d’ is also wrong.
⇒ Only option left is ‘c’
But, I will show that it is also right.
When VAB = 2.δ V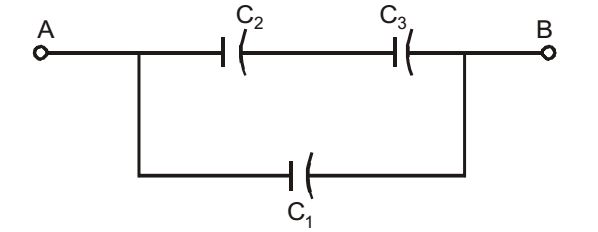
voltage across C1 = 2.8 V [possible as breakdown voltage is 10 V].V2 = C3 × 2.8 C2 + C3
[possible as breakdown voltage across C2 is 5V)]V2 = 0.8 V V3 = 
C2 
× 2.8 C2 + C3
= 2 V [possible as breakdown voltage across C3 is 2V] hence option ‘d’ is correct
*Verification : As I already showed that only ‘s’ is true no one else.
Conclusion :
is not same asvoltage across method capacitance
For determine voltage across resistance we just do as we want to determine across R1 & R2 .voltage across method resistance. 
But in capacitor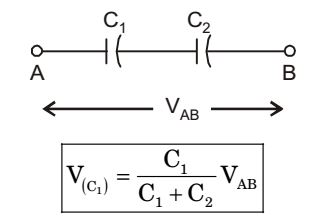
So, don’t apply resistance voltage method in to capacitor one, if you do that then you will obtain ‘D’ as answer, but which is wrong.
Correct Option: D
Given values :
Capacitance Value Voltage Breakdown C1 10 F 10V C2 5 F 5V C3 2 F 2V
Given circuit :
To find :
Max. safe voltage in volts that can be applied across the combination and Corresponding total charge is C.
Devising a plan :
(a) We will first calculate equivalent capacitance of given figure.
(b) By calculating capacitance, we can check which answer can be the solution, it reduce your effort in solving problem.
(c) Then apply the remaining answer for remaining options.
Solving :
Equivalent capacitance, as C2 & C3 are in series and we know that when capacitanceare in series equivalent capacitance = C2 C3 C2 + C3
& when two capacitor ar e in parallel then their addition= C1 + C2 C3 C2 + C3 * C = C1 + C2 C3 = 10μF + 5μF × 2μF = 11.4285 F C2 + C3 5μF + 2μF
Now check the option by using formula CV = θ
(a) 2.8 × 11.4285 = 32 μC ≠ 36 μC (option (a) is wrong)
hence ‘c’ option can be right
Now when 7V
(b) 7V × 11.4285 F = 80 c ≠ 119 C {B is hence ‘d’ option is right. only ‘c’ & ‘d’ are left.
⇒ Now apply 7V first in given circuit,
when voltage across AB is 7V then C1 can handle it broz max breakdown voltage across is 10Y.
and across
as they are in series so charge across them will be same.
Q2 = Q3
C2 V2 = C3 V3
C2 V2 = C3 V3 [V2 + V3 = 7V]
C2 V2 = C3 (7 – V2)
C2 V2 = 7C3 – C3 V2V2 = 7 C3 C2 + C3 V2 = 7 × 2 = 2 V 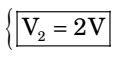
2 + 5
and V3 = 7 – V2 = 7 – 2V3 = 5 V
As when we take ‘7V’ then for that V2 = 2V & V3 = 5V, but max voltage across V3can be 2V [because above which it breakdown].
asV3 ≤ 2 V
But, when we take 7V then V3 have to be 5V which is not possible hence ‘d’ is also wrong.
⇒ Only option left is ‘c’
But, I will show that it is also right.
When VAB = 2.δ V
voltage across C1 = 2.8 V [possible as breakdown voltage is 10 V].V2 = C3 × 2.8 C2 + C3
[possible as breakdown voltage across C2 is 5V)]V2 = 0.8 V V3 = 
C2 
× 2.8 C2 + C3
= 2 V [possible as breakdown voltage across C3 is 2V] hence option ‘d’ is correct
*Verification : As I already showed that only ‘s’ is true no one else.
Conclusion :
is not same asvoltage across method capacitance
For determine voltage across resistance we just do as we want to determine across R1 & R2 .voltage across method resistance. 
But in capacitor
So, don’t apply resistance voltage method in to capacitor one, if you do that then you will obtain ‘D’ as answer, but which is wrong.

