1. C₀ is the capacitance of parallel plate capacitor with air as dielectric (as in figure (a)). If, half of the entire gap as shown in figure (b) is filled with a dielectric of permittivity ∈_r, the expression for the modified capacitance is
   
   

1. 1. C0	(1 + ∈r)
      2

      
      

   
   
   

   2. (C₀ + ∈_r)
      
      

   
   
   

   3. C0	∈r
      2

      
      

   
   
   

   4. C₀(1 + ∈_r)

   
   
   

---

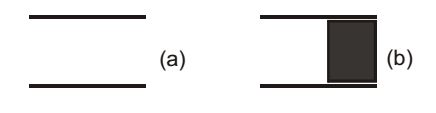
1. View Hint View Answer Discuss in Forum

   
   

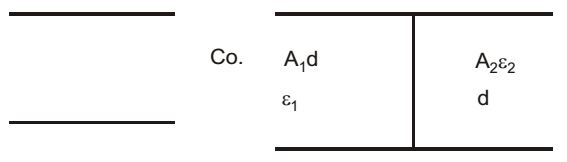
   C0 =	∈0 A
   	d

   
   Now C = C₁ + C₂
   

   ∴ C =	A1 ∈1	+	A2 ∈2
   	d		d

   
   

   =	A ∈0	+	A ∈r ∈0
   	2d		2d

   
   

   C =	A ∈0	(1 + ∈r)
   	2d

   
   

   C =	C0	(1 + ∈r)
   	2

   
   

   (∵ C0 =	A ∈0	)
   	d

   
   

   Correct Option: A

   
   

   C0 =	∈0 A
   	d

   
   Now C = C₁ + C₂
   

   ∴ C =	A1 ∈1	+	A2 ∈2
   	d		d

   
   

   =	A ∈0	+	A ∈r ∈0
   	2d		2d

   
   

   C =	A ∈0	(1 + ∈r)
   	2d

   
   

   C =	C0	(1 + ∈r)
   	2

   
   

   (∵ C0 =	A ∈0	)
   	d

   
   

---

2. If two-port network shown in the given figure has the constant B =	2s + 1
   	s2

   
   then z(s) will be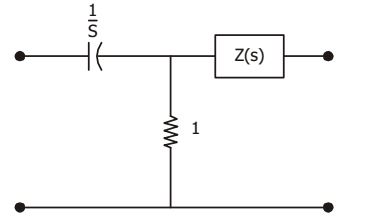
   
   

1. 1. s
      

   
   
   

   2. 	1
      	s

      
      

   
   
   

   3. s + 1
      

   
   
   

   4. 1 +	1
      	s

      
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
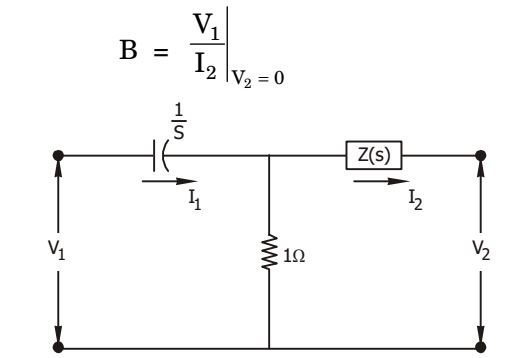
   If V₂ = 0, then
   

   I1(s) =	V1 (s)
   	Z (s)	+	1
   	Z (s) + 1		s

   
   

   and I2 (s) = I1 ×	1	=	V1(s).s
   	Z(s) + 1		sZ(s) + [1 + Z(s)]

   
   

   Given : B =	2s + 1
   	s2

   
   

   ∴	V1(s)	=	sZ(s) + (1 + V(s))	=	2	+	1
   	I2(s)		s		s		s2

   
   

   ⇒	(s + 1)z(s)	=	(s + 1)
   	s		s2

   
   

   ⇒ Z(s) =	1
   	s

   
   

   Correct Option: B

   
   If V₂ = 0, then
   

   I1(s) =	V1 (s)
   	Z (s)	+	1
   	Z (s) + 1		s

   
   

   and I2 (s) = I1 ×	1	=	V1(s).s
   	Z(s) + 1		sZ(s) + [1 + Z(s)]

   
   

   Given : B =	2s + 1
   	s2

   
   

   ∴	V1(s)	=	sZ(s) + (1 + V(s))	=	2	+	1
   	I2(s)		s		s		s2

   
   

   ⇒	(s + 1)z(s)	=	(s + 1)
   	s		s2

   
   

   ⇒ Z(s) =	1
   	s

   
   

---

---

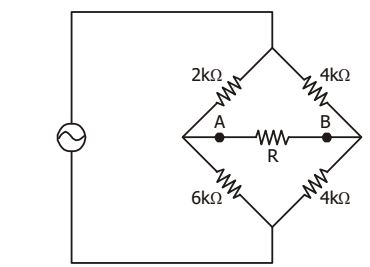
3. Value of the resistance R, connected across the terminals A and B, (see given figure), which will absorb maximum power, is __________ kΩ
   
   

1. 1. 4.00

   
   
   

   2. 8

   
   
   

   3. 64

   
   
   

   4. None of the above

   
   
   

---

1. View Hint View Answer Discuss in Forum

   The circuit is drawn below by shorting the voltage source.
   
   Taking Thevenin's equivalent between points A, B, we have
   

   RTh =		6 × 3	+	4 × 4		kΩ = 4 kΩ
   		6 + 3		4 + 4

   
   For maximum power transfer, R = R_Th = 4kΩ

   Correct Option: A

   The circuit is drawn below by shorting the voltage source.
   
   Taking Thevenin's equivalent between points A, B, we have
   

   RTh =		6 × 3	+	4 × 4		kΩ = 4 kΩ
   		6 + 3		4 + 4

   
   For maximum power transfer, R = R_Th = 4kΩ

---

4. For the circuit shown in the given figure, if input impedance Z₁ at port 1 is given by
   

   Z1 = K1	(s + 2)
   	s + 5

   
   then input impedance Z₂ at port 2 will be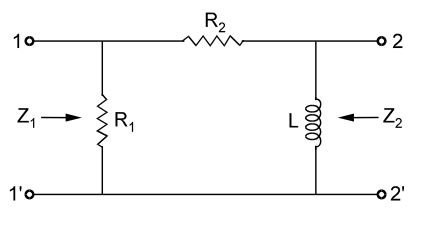
   
   

1. 1. 	K2(s + 3)
      	s + 5

      
      

   
   
   

   2. 	K2(s + 2)
      	s + 3

      
      

   
   
   

   3. 	K2 s
      	s + 5

      
      

   
   
   

   4. 	K2 s
      	s + 2

      
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Z1 = K1	(s + 2)
   	s + 5

   
   

   ∴ Z1 = R1	(R2 + Ls)
   	R1 + R2 + Ls

   
   

   =	R1L			R2
   				L + (s)
   	L			R1 + R2
   				L + (s)

   
   

   =	R1			R2
   				L + (s)
   				R1 + R2
   				L + (s)

   
   ∴ R₁ = K₁
   

   	R2	= 2 ,	R1 + R2	= 5
   	L		L

   
   

   Again , R2 =	2	K1 , L =	K
   	3		3

   
   

   ∴ Z2 =	Ls(R1 + R2)
   	Ls + R2Cs

   
   

   =		K1				K1 + 2
   		3s				3K1
   		K1		sK1 +			2
   		3					3K1

   
   

   =	s		5
   			3K1		=	K2s
   			(s + 5)			(s + 5)

   
   

   ∴ K2 =	5	K1
   	3

   
   

   Correct Option: C

   Z1 = K1	(s + 2)
   	s + 5

   
   

   ∴ Z1 = R1	(R2 + Ls)
   	R1 + R2 + Ls

   
   

   =	R1L			R2
   				L + (s)
   	L			R1 + R2
   				L + (s)

   
   

   =	R1			R2
   				L + (s)
   				R1 + R2
   				L + (s)

   
   ∴ R₁ = K₁
   

   	R2	= 2 ,	R1 + R2	= 5
   	L		L

   
   

   Again , R2 =	2	K1 , L =	K
   	3		3

   
   

   ∴ Z2 =	Ls(R1 + R2)
   	Ls + R2Cs

   
   

   =		K1				K1 + 2
   		3s				3K1
   		K1		sK1 +			2
   		3					3K1

   
   

   =	s		5
   			3K1		=	K2s
   			(s + 5)			(s + 5)

   
   

   ∴ K2 =	5	K1
   	3

   
   

---

---

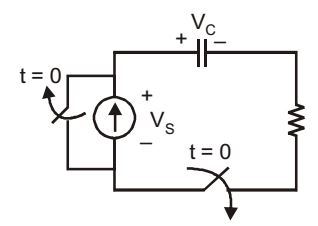
5. A combination of 1mF capacitor with an initial voltage v_c (0) = – 2V in series with a 100 Ω resistor is connected to a 20 mA ideal dc current source by operating both switches at t = 0s as shown. Which of the following graphs shown in the options approximates the voltage v_s across the current source over the next few second?
   
   

1. 1. 
      

   
   
   

   2. 
      

   
   
   

   3. 
      

   
   
   

   4. 
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Under steady state condition,
   
   When switch is opened :
   
   By using Laplace transform approach.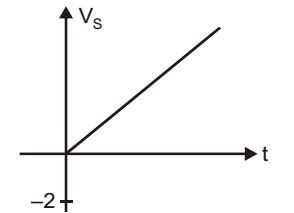
   
   

   V (S) =

   1

   1

   +

   1

   100 +

   -2

   S

   SC

   S

   S

   
   

   VS(S) =	20 × 103
   	S2

   
   

   ⇒ VS(S) =	2 × 104
   	S2

   
   V_S(t) = 2 × 10⁴
   

   Correct Option: C

   Under steady state condition,
   
   When switch is opened :
   
   By using Laplace transform approach.
   
   

   V (S) =

   1

   1

   +

   1

   100 +

   -2

   S

   SC

   S

   S

   
   

   VS(S) =	20 × 103
   	S2

   
   

   ⇒ VS(S) =	2 × 104
   	S2

   
   V_S(t) = 2 × 10⁴
   

---