Electric circuits miscellaneous
- Assuming both the voltage sources are in phase, the value of R for which maximum power is transferred from circuit A to circuit B is

-
View Hint View Answer Discuss in Forum
Power transferred from circuit A to circuit B
P = VI = 
7 
. 
6 + 10R 
= 42 + 70R R + 2 R + 2 (R + 2)2 I = 10 - 3 = 7 2 + R 2 + R V = 3 + IR = 3 + 7R = 6 + 10R 2 + R 2 + R ∴ dP = (R + 2)2(70) - (42 + 70R) 2 (R + 2) = 0 dR (R + 2)4 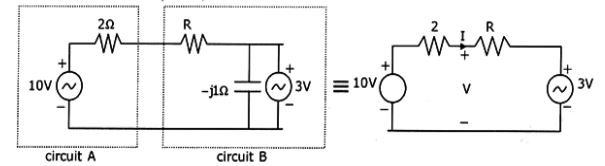
⇒ 70(R + 2)2 = (42 + 70R) 2 (R + 2)
⇒ 5(R + 2) = 2(3 + 5R)
⇒ 5R + 10 = 6 + 10R
4 = 5R
⇒ R = 0.8 Ω
Correct Option: A
Power transferred from circuit A to circuit B
P = VI = 
7 
. 
6 + 10R 
= 42 + 70R R + 2 R + 2 (R + 2)2 I = 10 - 3 = 7 2 + R 2 + R V = 3 + IR = 3 + 7R = 6 + 10R 2 + R 2 + R ∴ dP = (R + 2)2(70) - (42 + 70R) 2 (R + 2) = 0 dR (R + 2)4 
⇒ 70(R + 2)2 = (42 + 70R) 2 (R + 2)
⇒ 5(R + 2) = 2(3 + 5R)
⇒ 5R + 10 = 6 + 10R
4 = 5R
⇒ R = 0.8 Ω
-
of the periodic signal shown below will contain the following nonzero termsThe Fourier series expansion 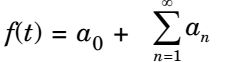
cos nωt + bn sin nωt 
-
View Hint View Answer Discuss in Forum
The given periodic signal is even as f(– t) = f(t) and also holes half-wave symmetry since
f 
t + T 
= f(t) 2
Hence, the signal will only have cosine terms and only odd harmonics will be present.
i.e. bn = 0
an = 0
for n = 2, 4, 6,... ∞ .
Hence the correct choice is (d).Correct Option: D
The given periodic signal is even as f(– t) = f(t) and also holes half-wave symmetry since
f 
t + T 
= f(t) 2
Hence, the signal will only have cosine terms and only odd harmonics will be present.
i.e. bn = 0
an = 0
for n = 2, 4, 6,... ∞ .
Hence the correct choice is (d).
- H ow many 200W/220V incandescent lamps connected in series would consume the same total power as a single 100W/220V incandescent lamp?
-
View Hint View Answer Discuss in Forum
V1 = V2 = Vn = 200 n
Power consumed in n bulbs connected in series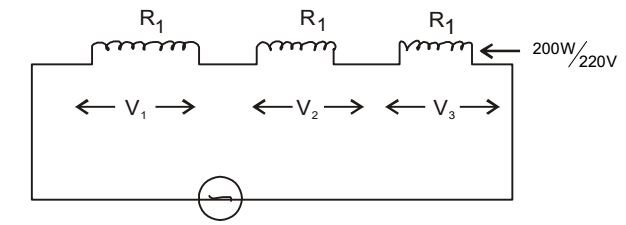
P1 = n. 
200 
2 . 1 = (200)2 n R1 nR1 But R1 = (200)2 200 ∴ P1 = 200 n
It must be equal to 100 watts (for bulb 100W/220V)∴ 200 = 100 n
or n = 2Correct Option: D
V1 = V2 = Vn = 200 n
Power consumed in n bulbs connected in series
P1 = n. 
200 
2 . 1 = (200)2 n R1 nR1 But R1 = (200)2 200 ∴ P1 = 200 n
It must be equal to 100 watts (for bulb 100W/220V)∴ 200 = 100 n
or n = 2
- The number of chords in the graph of the given circuit will be
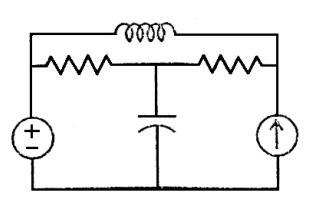
-
View Hint View Answer Discuss in Forum
Network Graph of given circuit is
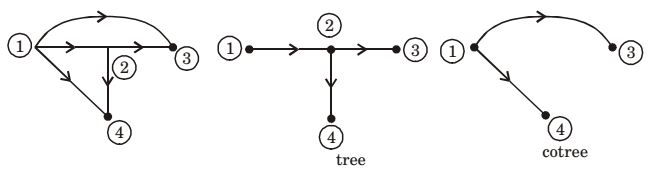
∴ Number of chords = branches of tree = 2
Since there is no option which has answer 2, so closest answer is 3.
Alternately
Opening up current source and short-circuiting voltage source, we have the graph as follows,
Correct Option: A
Network Graph of given circuit is

∴ Number of chords = branches of tree = 2
Since there is no option which has answer 2, so closest answer is 3.
Alternately
Opening up current source and short-circuiting voltage source, we have the graph as follows,
- The parameter type and the matrix representation of the relevant two port parameters that describe the circuit shown are

-
View Hint View Answer Discuss in Forum
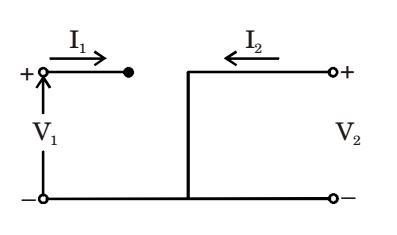
I1 = g11 V1 + g12 I2
V2 = g21 V1 + g22 I2
I1 = 0 [port-1 open-circuited]
V2 = 0 [port-2 short-circuited]
g22 = 0 = 0 I2
G-parameters, are= 
g11 g12 
= 
0 0 
g21 g22 0 0
Correct Option: C

I1 = g11 V1 + g12 I2
V2 = g21 V1 + g22 I2
I1 = 0 [port-1 open-circuited]
V2 = 0 [port-2 short-circuited]
g22 = 0 = 0 I2
G-parameters, are= 
g11 g12 
= 
0 0 
g21 g22 0 0

