-
of the periodic signal shown below will contain the following nonzero termsThe Fourier series expansion 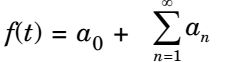
cos nωt + bn sin nωt 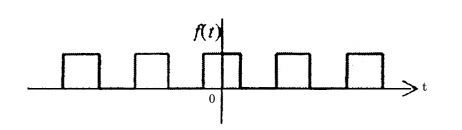
-
- a0 and bn , n = 1, 3, 5, ....... ∞
- a0 and an , n = 1, 2, 3,.... ∞
- a0, an and bn, n = 1, 2, 3,... ∞
- a0 and an, n = 1, 3, 5,... ∞
Correct Option: D
The given periodic signal is even as f(– t) = f(t) and also holes half-wave symmetry since
| f |  | t + |  | = f(t) | |
| 2 |
Hence, the signal will only have cosine terms and only odd harmonics will be present.
i.e. bn = 0
an = 0
for n = 2, 4, 6,... ∞ .
Hence the correct choice is (d).

