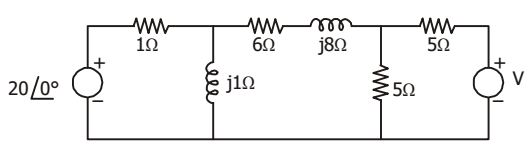
1. In the given circuit, if the power dissipated in the 6 Ω resistor is zero then V is
   
   

1. 1. 20 √2 ∠ 45°
      

   
   
   

   2. 20 ∠ 30°
      

   
   
   

   3. 20 ∠ 45°
      

   
   
   

   4. 20 √2 ∠ 30°
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   From the circuit, 20 ∠ 0° = I₁ (1 + j)
   

   ⇒ I1 =	20
   	1 + j

   
   

   and, 20 ∠ 0° = I1 + 5I2 =	20	+ 5I2
   	1 + j

   
   

   ⇒ 5I2 =	20
   	1 + j

   
   

   Then , V = 10I2 = 2 .	20	=	40j
   	1 + j		1 + j

   
   = 20 √2 ∠ 45°
   

   Correct Option: A

   
   From the circuit, 20 ∠ 0° = I₁ (1 + j)
   

   ⇒ I1 =	20
   	1 + j

   
   

   and, 20 ∠ 0° = I1 + 5I2 =	20	+ 5I2
   	1 + j

   
   

   ⇒ 5I2 =	20
   	1 + j

   
   

   Then , V = 10I2 = 2 .	20	=	40j
   	1 + j		1 + j

   
   = 20 √2 ∠ 45°
   

---

2. In the circuit shown in the given figure, switch K is closed at t = 0. The circuit was initially relaxed. Which one of the following sources of v(t) will produce maximum current at t = 0⁺ ?
   
   

1. 1. Unit step

   
   
   

   2. Unit impulse

   
   
   

   3. Unit ramp

   
   
   

   4. Unit step plus unit ramp

   
   
   

---

1. View Hint View Answer Discuss in Forum

   For unit step source,
   

   I(t) =	V		1 - e(-R / L)t
   	R

   
   At t = 0, I (t) = 0
   

   For ramp, inputI (t) I(t) =	V		tUt -		1 - e(-R / L)t
   	R

   
   At t = 0, I(t) = 0
   

   For impulse input, I(t) =	V	e(-R / L)t
   	R

   
   

   Then at t = 0, I(t) =	V	Maximum
   	R

   
   

   Correct Option: B

   For unit step source,
   

   I(t) =	V		1 - e(-R / L)t
   	R

   
   At t = 0, I (t) = 0
   

   For ramp, inputI (t) I(t) =	V		tUt -		1 - e(-R / L)t
   	R

   
   At t = 0, I(t) = 0
   

   For impulse input, I(t) =	V	e(-R / L)t
   	R

   
   

   Then at t = 0, I(t) =	V	Maximum
   	R

   
   

---

---

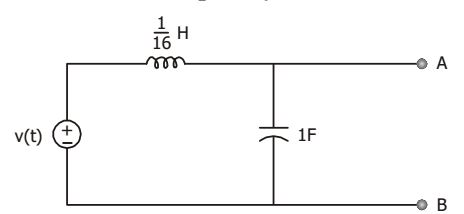
3. The circuit shown in the given figure, will act as an ideal current source with respect to terminal A and B, when frequency is
   
   

1. 1. zero

   
   
   

   2. 1 rad/s

   
   
   

   3. 4 rad/s

   
   
   

   4. 16 rad/s

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Redrawing equivalent circuit
   
   
   

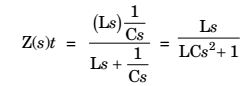
   ⇒ Z(jω) =	jωL
   	1 - LCω2

   
   For ideal current source, Z(jω) = ∞
   ⇒ 1 – LCω² = 0
   

   ⇒ ω =	1	= 4 rad /sec
   	√LC

   Correct Option: C

   Redrawing equivalent circuit
   
   
   

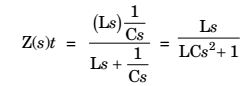
   ⇒ Z(jω) =	jωL
   	1 - LCω2

   
   For ideal current source, Z(jω) = ∞
   ⇒ 1 – LCω² = 0
   

   ⇒ ω =	1	= 4 rad /sec
   	√LC

---

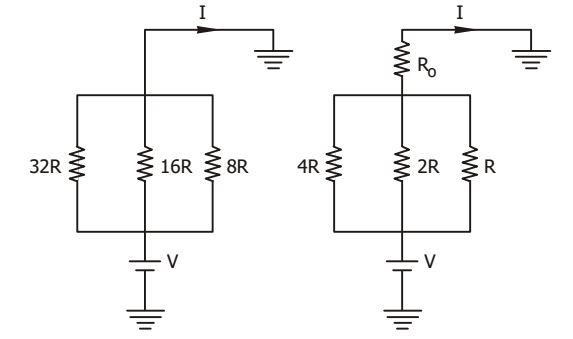
4. The circuit shown in Fig-I is replaced by that in FigII. If current I remains the same, then R₀ will be
   
   

1. 1. zero
      

   
   
   

   2. R
      

   
   
   

   3. 2R
      

   
   
   

   4. 4R

   
   
   

---

1. View Hint View Answer Discuss in Forum

   From Fig. (a),
   

   I =	V	+	V	+	V	=	7V
   	32R		16R		8R		32R

   
   From Fig. (b),
   

   I = (V - IR0)		1	+	1	+	1		=	7(V- IR0)
   		4R		2R		R			4R

   
   Since current remains same
   

   ∴	7(V- IR0)	=	7V
   	4R		32R

   
   

   ⇒ (V- IR0) =	V
   	8

   
   

   ⇒ IR0 =	7V	= 4R.I
   	8

   
   ⇒ R₀ = 4R

   Correct Option: D

   From Fig. (a),
   

   I =	V	+	V	+	V	=	7V
   	32R		16R		8R		32R

   
   From Fig. (b),
   

   I = (V - IR0)		1	+	1	+	1		=	7(V- IR0)
   		4R		2R		R			4R

   
   Since current remains same
   

   ∴	7(V- IR0)	=	7V
   	4R		32R

   
   

   ⇒ (V- IR0) =	V
   	8

   
   

   ⇒ IR0 =	7V	= 4R.I
   	8

   
   ⇒ R₀ = 4R

---

---

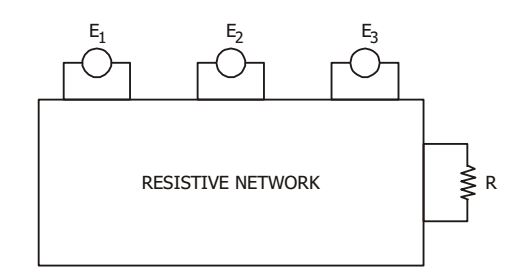
5. In the circuit given in the figure, the power consumed in the resistance R is measured when one source is acting at a time, these values are 18 W, 50 W and 98 W. When all the sources are acting simultaneously, possible maximum and minimum values of power in R will be
   
   

1. 1. 98 W and 18 W

   
   
   

   2. 166 W and 18 W

   
   
   

   3. 450 W and 2 W

   
   
   

   4. 166 W and 2 W

   
   
   

---

1. View Hint View Answer Discuss in Forum

   P1 = 18 =	E12
   	R

   
   

   P2 = 50 =	E22
   	R

   
   

   P3 = 98 =	E32
   	R

   
   

   Maximum power, Pmax =	(E1 + E2 + E3)2
   	R

   
   

   =	E12 + E22 + E32 + 2E1E2 + 2E2E3 + 2E3E1
   	R

   
   ⇒ P_max = P₁ + P₂ + P₃ + 2(√P₁P₂ + √P₂P₃ + √P₃P₁)
   = 18 + 50 + 98 + 2 √18 × 50 + 2 √50 × 98 + 2 √18 × 98 = 450 watts
   

   Minimum power, Pmax =	(E1 - E2 - E3)2
   	R

   
   = P₁ + P₂ + P₃ - 2√P₁P₃ - 2√P₂P₃ + 2√P₁P₂)
   = 18 + 50 + 98 - 2 √18 × 98 - 2 √50 × 98 + 2 √18 × 50 = 2 watts
   

   Correct Option: C

   P1 = 18 =	E12
   	R

   
   

   P2 = 50 =	E22
   	R

   
   

   P3 = 98 =	E32
   	R

   
   

   Maximum power, Pmax =	(E1 + E2 + E3)2
   	R

   
   

   =	E12 + E22 + E32 + 2E1E2 + 2E2E3 + 2E3E1
   	R

   
   ⇒ P_max = P₁ + P₂ + P₃ + 2(√P₁P₂ + √P₂P₃ + √P₃P₁)
   = 18 + 50 + 98 + 2 √18 × 50 + 2 √50 × 98 + 2 √18 × 98 = 450 watts
   

   Minimum power, Pmax =	(E1 - E2 - E3)2
   	R

   
   = P₁ + P₂ + P₃ - 2√P₁P₃ - 2√P₂P₃ + 2√P₁P₂)
   = 18 + 50 + 98 - 2 √18 × 98 - 2 √50 × 98 + 2 √18 × 50 = 2 watts
   

---