Electric circuits miscellaneous Easy Questions and Answers | Page - 34

Electric circuits miscellaneous

In the following figure, C₁ and C₂ are ideal capacitors. C₁ has been charged to 12V before the ideal switch S is closed at t = 0. The curent i(t) for all t is

1. zero
1. a step function
1. an exponentially decaying function
1. an impulse function

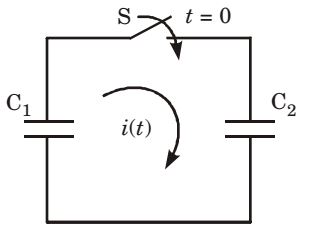
View Hint View Answer Discuss in Forum

Time constant = RC
In the given circuit, R = 0
∴ Rise time = 0;
hence capacitor charges instantaneously and current can be represented as impulse function.

Correct Option: D

Time constant = RC
In the given circuit, R = 0
∴ Rise time = 0;
hence capacitor charges instantaneously and current can be represented as impulse function.

The circuit shown in the figure given below is energized by a sinusoidal voltage source V₁ at a frequency which causes resonance with a current of I.

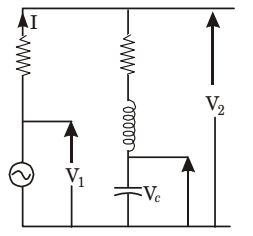
The phasor diagram which is applicable to this circuit is

View Hint View Answer Discuss in Forum

At resonance, voltage across L and C will be equal in magnitude and opposite in direction. So V₂ is the voltage which is equal to the voltage across R₁, and will be in the same direction of I and V₁ be voltage across capacitor V_c will be lagging the current by 90°.
Thus, we have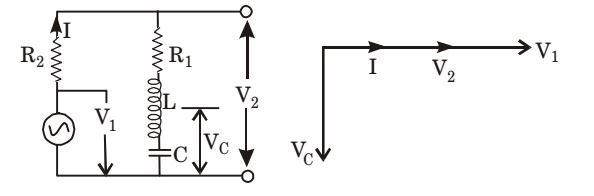

Correct Option: A

At resonance, voltage across L and C will be equal in magnitude and opposite in direction. So V₂ is the voltage which is equal to the voltage across R₁, and will be in the same direction of I and V₁ be voltage across capacitor V_c will be lagging the current by 90°.
Thus, we have

The circuit shown is a

1. low pass filter with f_3dB = 1 rad / s
  (R₁ + R₂)C
1. high pass filter with f_3dB = 1 rad / s
  R₁C
1. low pass filter with f_3dB = 1 rad / s
  R₁C
1. high pass filter with f_3dB = 1 rad / s
  (R₁ + R₂)C

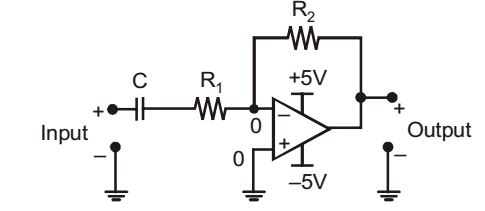
View Hint View Answer Discuss in Forum

V_o = - R₂
V_in R₁ + 1
sC₁

= - sC₁R₂
sC₁R₁ + 1

It is HPF transfer function .

Correct Option: B

V_o = - R₂
V_in R₁ + 1
sC₁

= - sC₁R₂
sC₁R₁ + 1

It is HPF transfer function .

The rms value of the current i(t) in the circuit shown below is

1. 1 A
  2
1. 1 A
  √2
1. 1 A
1. √2 A

View Hint View Answer Discuss in Forum

ω = 1 rad / sec
X_L = 1 Ω ; X_C = 1 Ω

I(t) = sin t = sin t
1 Ω

I_rms = 1 A
√2

Correct Option: B

ω = 1 rad / sec
X_L = 1 Ω ; X_C = 1 Ω

I(t) = sin t = sin t
1 Ω

I_rms = 1 A
√2

Divergence of the three-dimensional radial vector field ^{^→}r is

1. 3
1. 1 / r

View Hint View Answer Discuss in Forum

Let three dimensional field, ^{^→}r = xî + yĵ + zk̂
∴ ∇ .^{^→}r = d î + d ĵ + d k̂ .(xî + yĵ + zk̂)
dx dy dz

⇒ ∇ = d . x + d . y + d . z
dx dy dz

= 1 + 1 + 1 = 3

Correct Option: A

Let three dimensional field, ^{^→}r = xî + yĵ + zk̂
∴ ∇ .^{^→}r = d î + d ĵ + d k̂ .(xî + yĵ + zk̂)
dx dy dz

⇒ ∇ = d . x + d . y + d . z
dx dy dz

= 1 + 1 + 1 = 3