Electric circuits miscellaneous

Electric circuits miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Electric Circuits

Electric circuits miscellaneous
  1. The sinusoidal steady-state voltage gain of the network shown in the given figure will have magnitude equal to 0.707 at an angular frequency of









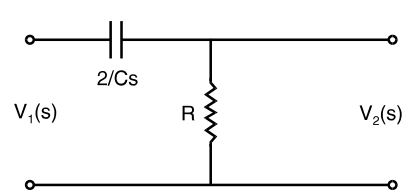
  1. View Hint View Answer Discuss in Forum



    M(jω) =
    V2(jω)
    V1(jω)

    Correct Option: C



    M(jω) =
    V2(jω)
    V1(jω)

  1. For the circuit shown in the figure, the current I is









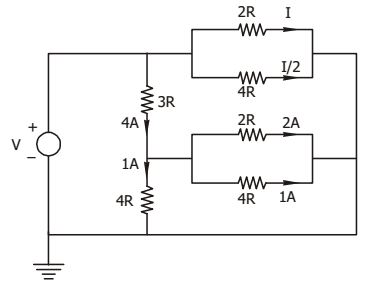
  1. View Hint View Answer Discuss in Forum

    Redrawing the circuit, we have

    From the circuit, V = 2RI ....(i)
    and, V = (3R)4 + (4R). 1 = 16 R ....(ii)
    From equations (i) and (ii), we get I = 8A

    Correct Option: D

    Redrawing the circuit, we have

    From the circuit, V = 2RI ....(i)
    and, V = (3R)4 + (4R). 1 = 16 R ....(ii)
    From equations (i) and (ii), we get I = 8A

  1. If a resistance R of 1 Ω is connected across the terminals AB as shown in the given figure, then the current flowing through R will be










  1. View Hint View Answer Discuss in Forum

    Shorting the voltage source and opening current source, we have ZTH = 1 Ω looking left into terminal AB.

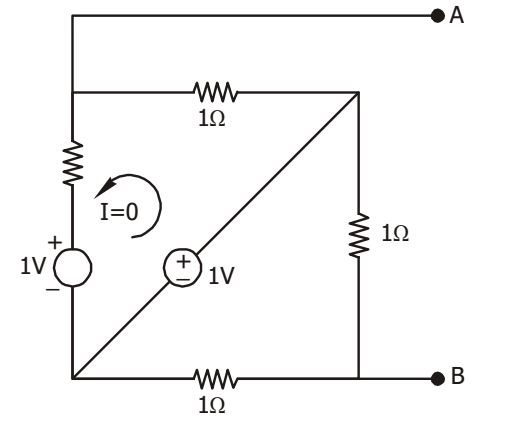
    Now, for VTH, from the circuit, we have
    VAB = VTH = 1 volt
    Then, current through R

    =
    VAB
    		 =
    1
    		 = 0.54
    R + ZTH2

    Correct Option: B

    Shorting the voltage source and opening current source, we have ZTH = 1 Ω looking left into terminal AB.

    Now, for VTH, from the circuit, we have
    VAB = VTH = 1 volt
    Then, current through R

    =
    VAB
    		 =
    1
    		 = 0.54
    R + ZTH2

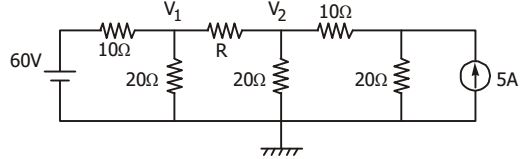
  1. In the given circuit, V1 = 40 V when R is 10 Ω . When R is zero, the value of V2 will be









  1. View Hint View Answer Discuss in Forum

    Applying KCL at node (1), we have

    V1 - 60
    		 +
    V1
    		 +
    V1 - V2
    		 = 0
    1020R

    ⇒
    V1 - 60
    		 +
    V1
    		 +
    V1
    		 =
    V2
    1020RR

    ⇒ V2 =
    V1 - 60
    		 +
    V1
    		R + V2
    1020

    R = 0 gives, V2 = V1
    Also ,
    V1 - 60
    		 +
    V1
    		 = 0
    1020

    ⇒ V1 = 40 volts
    ∴ V2 = 0 V

    Correct Option: A

    Applying KCL at node (1), we have

    V1 - 60
    		 +
    V1
    		 +
    V1 - V2
    		 = 0
    1020R

    ⇒
    V1 - 60
    		 +
    V1
    		 +
    V1
    		 =
    V2
    1020RR

    ⇒ V2 =
    V1 - 60
    		 +
    V1
    		R + V2
    1020

    R = 0 gives, V2 = V1
    Also ,
    V1 - 60
    		 +
    V1
    		 = 0
    1020

    ⇒ V1 = 40 volts
    ∴ V2 = 0 V

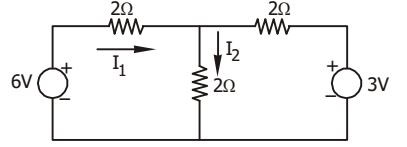
  1. In the circuit shown in the given figure, if I1 = 1.5 A, then I2 will be









  1. View Hint View Answer Discuss in Forum

    From the circuit, we have
    6 = 2I1 + 2I2
    ⇒ I2 = 1.5A

    Correct Option: C

    From the circuit, we have
    6 = 2I1 + 2I2
    ⇒ I2 = 1.5A