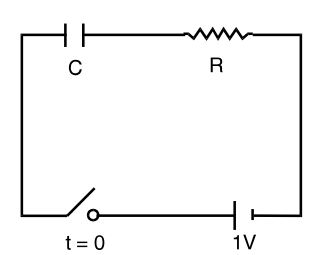
81. In the series Rc circuit shown in the figure, the voltage across C starts increasing when the d.c. source is switched on. The rate of increase of voltage across C at the instant just after the switch is closed (i.e. at t = 0⁺) will be
    
    

1. 1. zero

   
   
   

   2. infinity

   
   
   

   3. RC

   
   
   

   4. 1
      RC

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Voltage across the capacitor at any time t, V_c = V (l – e^{– t / RC})
   = l – e^{– t / RC} ... (since V = 1 volt)
   

   ∴	dVc	=	1	e– t / RC
   	dt		RC

   
   

   At t = 0+ ,	dVc	=	1
   	dt		RC

   
   

   Correct Option: D

   Voltage across the capacitor at any time t, V_c = V (l – e^{– t / RC})
   = l – e^{– t / RC} ... (since V = 1 volt)
   

   ∴	dVc	=	1	e– t / RC
   	dt		RC

   
   

   At t = 0+ ,	dVc	=	1
   	dt		RC

   
   

---

82. A periodic rectangular signal X(t) has the wave form shown in the figure. Frequency of the fifth harmonic of its spectrum is
    
    

1. 1. 40 Hz

   
   
   

   2. 200 Hz

   
   
   

   3. 250 Hz

   
   
   

   4. 1250 Hz

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Periodic time = 4 ms = 4 × 10 ^{– 3} sec.
   

   Fundamental frequency =	103	= 250 Hz
   	4

   
   ∴ Frequency of the 5th harmonic = 250 × 5 = 1250 Hz
   

   Correct Option: D

   Periodic time = 4 ms = 4 × 10 ^{– 3} sec.
   

   Fundamental frequency =	103	= 250 Hz
   	4

   
   ∴ Frequency of the 5th harmonic = 250 × 5 = 1250 Hz
   

---

---

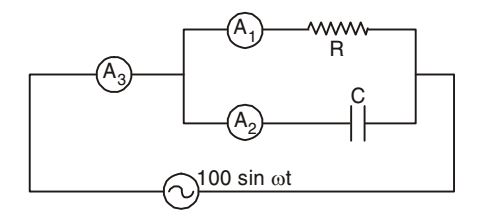
83. In the given figure, A₁, A₂ and A₃ are ideal ammeters. If A₁ reads 5A, A₂ reads 12 A, then A₃ should read
    
    

1. 1. 7 A

   
   
   

   2. 12 A

   
   
   

   3. 13 A

   
   
   

   4. 17 A

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Since the source is an a.c voltage, therefore
   I _3rms = √I_1rms ² + I_2rms ²
   = √5² +12² = 13 A

   Correct Option: C

   Since the source is an a.c voltage, therefore
   I _3rms = √I_1rms ² + I_2rms ²
   = √5² +12² = 13 A

---

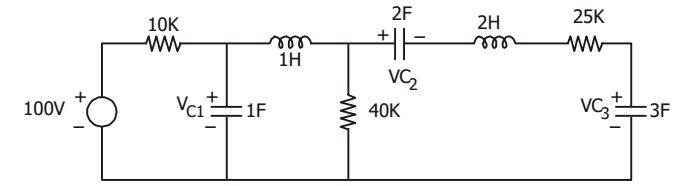
84. The voltage V_C1, V_C2 and V_C3 across the capacitors in the circuit in the given figure, under steady state are respectively
    
    

1. 1. 80 V, 32 V, 48 V

   
   
   

   2. 80 V, 48 V, 32 V

   
   
   

   3. 20 V, 8 V, 12 V

   
   
   

   4. 20 V, 12 V, 8 V

   
   
   

---

1. View Hint View Answer Discuss in Forum

   In steady state, capacitors are open and inductances are short.
   
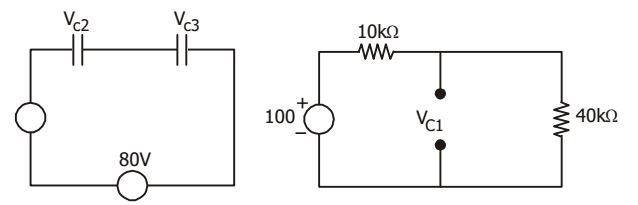
   For V_C1
   

   VC1 = 100 ×	40	= 80 V
   	50

   
   For V_C2 and V_C3
   

   VC2 = 80 ×	C3
   	C2 + C3

   
   

   = 80 ×	3	= 48 V
   	5

   
   

   VC3 = 80 ×	C2
   	C2 + C3

   
   = 16 × 2 = 32 V
   

   Correct Option: B

   In steady state, capacitors are open and inductances are short.
   
   For V_C1
   

   VC1 = 100 ×	40	= 80 V
   	50

   
   For V_C2 and V_C3
   

   VC2 = 80 ×	C3
   	C2 + C3

   
   

   = 80 ×	3	= 48 V
   	5

   
   

   VC3 = 80 ×	C2
   	C2 + C3

   
   = 16 × 2 = 32 V
   

---

---

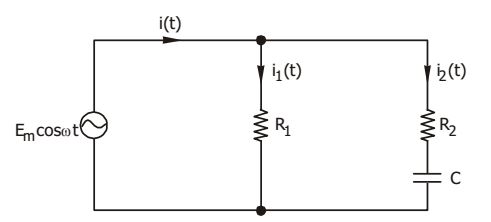
85. When the angular frequency ω in the given figure is varied from 0 to ∞ , the locus of the current phasor I₂ is given by
    

1. 1. 
      

   
   
   

   2. 
      

   
   
   

   3. 
      

   
   
   

   4. 

   
   
   

---

1. View Hint View Answer Discuss in Forum

   I2(ω) =	Em cosωt
   	R2 +	1
   		jωC

   
   
   
   

   At ω = ∞ , I2ω =	Em
   	R2

   
   Also, I₂ is leading with voltage phasor.
   At ω = 0, I₂ (0) = 0
   Thus desired locus should be as shown.

   Correct Option: A

   I2(ω) =	Em cosωt
   	R2 +	1
   		jωC

   
   
   
   

   At ω = ∞ , I2ω =	Em
   	R2

   
   Also, I₂ is leading with voltage phasor.
   At ω = 0, I₂ (0) = 0
   Thus desired locus should be as shown.

---