221. The power delivered by the current source, in the figure, is ________.
     

1. 1. 0 Watts

   
   
   

   2. 3 Watts

   
   
   

   3. 9 Watts

   
   
   

   4. 27 Watts

   
   
   

---

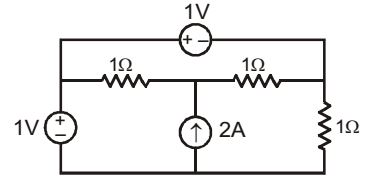
1. View Hint View Answer Discuss in Forum

   
   KCL at node V_x :
   

   	1 - Vx	+ 2 =	Vx
   	1		1

   
   

   Vx = 1.5 V

   
   Power delivered by current source is = 2 × 1.5 = 3 watts

   Correct Option: B

   
   KCL at node V_x :
   

   	1 - Vx	+ 2 =	Vx
   	1		1

   
   

   Vx = 1.5 V

   
   Power delivered by current source is = 2 × 1.5 = 3 watts

---

222. The time constant of the network shown in the figure is
     
     

1. 1. 2RC
      

   
   
   

   2. 3RC
      

   
   
   

   3. 	RC
      	2

      
      

   
   
   

   4. 	2RC
      	3

      
      

   
   
   

---

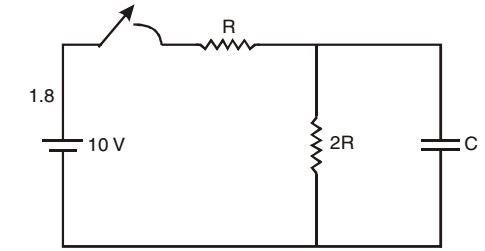
1. View Hint View Answer Discuss in Forum

   
   

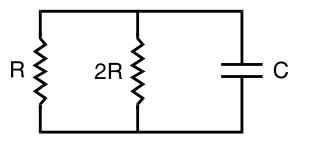
   Req =	R × 2R	=	2R
   	3R		3

   
   

   τ = Req × C =	2	R × C =	2	RC
   	3		3

   Correct Option: D

   
   

   Req =	R × 2R	=	2R
   	3R		3

   
   

   τ = Req × C =	2	R × C =	2	RC
   	3		3

---

---

223. Two coils having equal resistance but different inductances are connected in series. the time constant of the series combination is the
     

1. 1. sum of the time constants of the individual coils

   
   
   

   2. average of the time constants of individual coils

   
   
   

   3. geometric mean of the time constants of the individual coils

   
   
   

   4. product of the time constants of the individual coils

   
   
   

---

1. View Hint View Answer Discuss in Forum

   T =	L1 + L2	=	L1 + L2	=	1		L1	+	L2
   	R1 + R2		2R2		2		R		R

   
   Thus time constant is the average of the time constant of individual coils.
   

   Correct Option: B

   T =	L1 + L2	=	L1 + L2	=	1		L1	+	L2
   	R1 + R2		2R2		2		R		R

   
   Thus time constant is the average of the time constant of individual coils.
   

---

224. When a unit impulse voltage is applied to an inductor of 1 H, the energy supplied by the source is
     
     

1. 1. ∞
      

   
   
   

   2. 1 J
      

   
   
   

   3. 	1	J
      	2

      
      

   
   
   

   4. 0
      

   
   
   

---

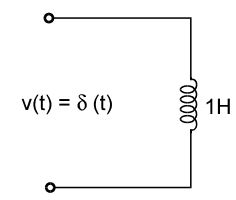
1. View Hint View Answer Discuss in Forum

   Current that flows is given by V (s) = sL I (s)
   ⇒ 1 = s.1. I(s)
   

   ⇒ I(s) =	1
   	s

   
   ∴ i(t) = u(t) = 1 Amp.
   

   Energy supplied =	1	LI2 =	1	× 1 × 1
   	2		2

   
   

   =	1	J
   	2

   
   

   Correct Option: C

   Current that flows is given by V (s) = sL I (s)
   ⇒ 1 = s.1. I(s)
   

   ⇒ I(s) =	1
   	s

   
   ∴ i(t) = u(t) = 1 Amp.
   

   Energy supplied =	1	LI2 =	1	× 1 × 1
   	2		2

   
   

   =	1	J
   	2

   
   

---

---

225. The circuit shown has i (t) = 10 sin (120 πt). The power (time average power) dissipated in R is
     

     C =	1	πH
     	60

     
     

     L =	1	πH
     	120

     
     R = 1ohm.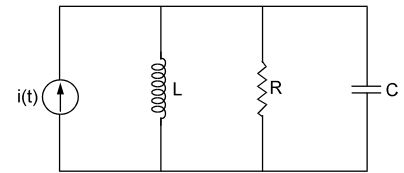
     
     

1. 1. 25 watts
      

   
   
   

   2. 100 watts
      

   
   
   

   3. 	10	watts
      	√2

      
      

   
   
   

   4. 50 watts

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using addition of admittances in parallel,
   

   Y = YL + YR + YC =	1	+ jωC = 1 + j
   	jωL

   
   The phasor voltage becomes
   

   V =	1
   	Y

   
   Using phasors in polar format,
   I = 10 e^{– jπ / 2}
   Y = √2 e^{– jπ / 4}
   Power (time average power) dissipated in R,
   

   P =	1	Re	(VV*)	= 25
   	2		R

   
   

   υ(t) =	10	cos		ωt -	3π
   	√2				4

   
   from which, P = (v)² (t) = 25 watts.

   Correct Option: A

   Using addition of admittances in parallel,
   

   Y = YL + YR + YC =	1	+ jωC = 1 + j
   	jωL

   
   The phasor voltage becomes
   

   V =	1
   	Y

   
   Using phasors in polar format,
   I = 10 e^{– jπ / 2}
   Y = √2 e^{– jπ / 4}
   Power (time average power) dissipated in R,
   

   P =	1	Re	(VV*)	= 25
   	2		R

   
   

   υ(t) =	10	cos		ωt -	3π
   	√2				4

   
   from which, P = (v)² (t) = 25 watts.

---