151. Which of the following statements holds for the divergence of electric and magnetic flux densities?
     

1. 1. Both are zero

   
   
   

   2. These are zero for static densities but non zero for time varying densities

   
   
   

   3. It is zero for the electric flux density

   
   
   

   4. It is zero for the magnetic flux density

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Divergence of magnetic field is always zero because magnetic flux makes always a closed path.
   So ∇ .B = 0 (Maxwell's equation),
   

   while divergence of electric field ∇ .E =	ρ
   	ε0

   
   

   Correct Option: D

   Divergence of magnetic field is always zero because magnetic flux makes always a closed path.
   So ∇ .B = 0 (Maxwell's equation),
   

   while divergence of electric field ∇ .E =	ρ
   	ε0

   
   

---

152. The parameters of the circuit shown in the figure given below are R_i = 1M Ω, R_o =10 Ω , A = 10⁶ V/V. If V_i = 1 μ V, then output voltage, input impedance and output impedance respectively are
     
     

1. 1. 1V, ∞, 10 Ω

   
   
   

   2. 1 V, 0, 10 Ω

   
   
   

   3. 1 V, 0, ∞

   
   
   

   4. 10 V, ∞, 10 Ω

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Output voltage= AV_i = 10⁶ × 10^{– 6} = 1 volt.
   V₁ = Z₁₁ i₁ + Z₁₂ i₂
   V₂ = Z₂₁ i₁ + Z₂₂ i₂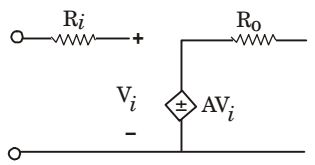
   
   Output circuit secondary, i₂ = 0
   

   Z22 =	V2	=	AVi	= R0 = 10 Ω
   	i2		i2

   
   

   Correct Option: A

   Output voltage= AV_i = 10⁶ × 10^{– 6} = 1 volt.
   V₁ = Z₁₁ i₁ + Z₁₂ i₂
   V₂ = Z₂₁ i₁ + Z₂₂ i₂
   
   Output circuit secondary, i₂ = 0
   

   Z22 =	V2	=	AVi	= R0 = 10 Ω
   	i2		i2

   
   

---

---

153. In the circuit shown in the figure given below, current source I = 1 A, voltage source V = 5V,
     R₁ = R₂ = R₃ = 1 W, L ₁ = L₂ = L ₃ = 1H, C₁ = C₂ = 1F.
     The currents (in A) through R₃ and the volt age source V respectively will be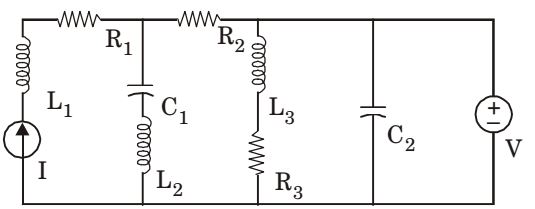
     
     

1. 1. 1, 4

   
   
   

   2. 5, 1

   
   
   

   3. 5, 2

   
   
   

   4. 5, 4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   At steady state, inductor gets short-circuited and capacitor gets open-circuited.
   
   Voltage across, R₃ = 5 volts
   

   Current through R3, I1 =	5	= 5 A
   	R3

   
   Given I₁ + I₂ = 1 A
   I₂ = 1 – I₁ = – 4 A
   (Current flowing in opposite direction)

   Correct Option: D

   At steady state, inductor gets short-circuited and capacitor gets open-circuited.
   
   Voltage across, R₃ = 5 volts
   

   Current through R3, I1 =	5	= 5 A
   	R3

   
   Given I₁ + I₂ = 1 A
   I₂ = 1 – I₁ = – 4 A
   (Current flowing in opposite direction)

---

154. Consider the following statements with reference to the equation	δp
     	δt

     
     1. This is a point form of the continuity equation
     2. Divergence of current density is equal to the decrease of charge per unit volume per unit at every point
     3. This is Max well's divergence equation
     4. This represents the conservation of charge Select the correct answer:
     

1. 1. Only 2 and 4 are true

   
   
   

   2. 1, 2 and 3 are true

   
   
   

   3. 2, 3 and 4 are true

   
   
   

   4. 1, 2 and 4 are true

   
   
   

---

1. View Hint View Answer Discuss in Forum

   ∇ .J =	δp
   	δt

   
   This a point form of continuity equation because divergence is a point fundamental property. This represents conservation of the charge. And divergence of current density is equal to decrease of charge per unit volume per unit at every point.

   Correct Option: D

   ∇ .J =	δp
   	δt

   
   This a point form of continuity equation because divergence is a point fundamental property. This represents conservation of the charge. And divergence of current density is equal to decrease of charge per unit volume per unit at every point.

---

---

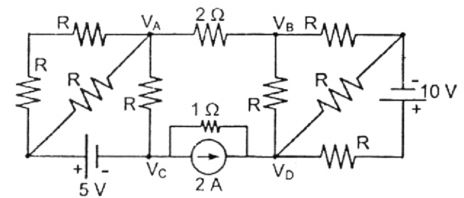
155. If V_A – V_B = 6V ; then V_C – V_D is
     
     

1. 1. – 5 V

   
   
   

   2. 2 V

   
   
   

   3. 3 V

   
   
   

   4. 6 V

   
   
   

---

1. View Hint View Answer Discuss in Forum

   I =	VA - VB	=	6	= 3 A ;
   	2		2

   
   Since current entering any network is same as leaving in V_C - V_D branch
   Also it is I = 3A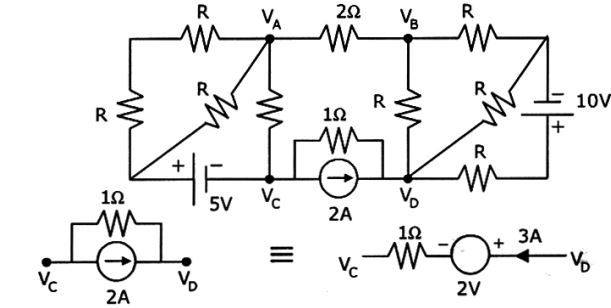
   
   V_D = 2 + 3 + V_C = 5 + V_C ;
   ∴ V_C – V_D = – 5V

   Correct Option: A

   I =	VA - VB	=	6	= 3 A ;
   	2		2

   
   Since current entering any network is same as leaving in V_C - V_D branch
   Also it is I = 3A
   
   V_D = 2 + 3 + V_C = 5 + V_C ;
   ∴ V_C – V_D = – 5V

---