111. A certain network N feeds a load resistance R as shown in the Fig. (a) It consumes a power of P W. If an identical network is added as shown in Fig. (b) then power consumed by R will be
     
     

1. 1. less than P

   
   
   

   2. equal to P

   
   
   

   3. between P and 4P

   
   
   

   4. more than 4P

   
   
   

---

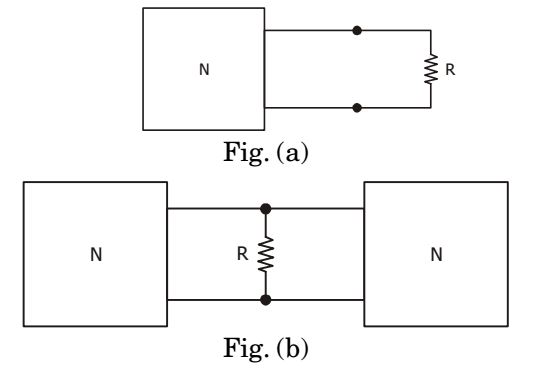
1. View Hint View Answer Discuss in Forum

   Let network N contains a resistance R and voltage V, then Fig. (a) is redrawn as below.
   
   

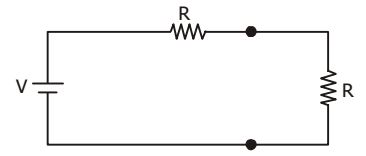
   and P =			V		2	=	V2
   			2R				4R

   
   Now, redrawing Fig. (b), we have
   power dissipated in R = P = V (2I)² R
   
   

   P' =			2V		2	R =	4V2	=	16	P
   			3R				9R		9

   
   Hence, P < P' < 4P

   Correct Option: C

   Let network N contains a resistance R and voltage V, then Fig. (a) is redrawn as below.
   
   

   and P =			V		2	=	V2
   			2R				4R

   
   Now, redrawing Fig. (b), we have
   power dissipated in R = P = V (2I)² R
   
   

   P' =			2V		2	R =	4V2	=	16	P
   			3R				9R		9

   
   Hence, P < P' < 4P

---

112. For a 2-port symmetrical bilateral network, if transmission parameters A = 3 and B = 1 Ω, then value of parameter C is
     

1. 1. 3 Ω

   
   
   

   2. 8 Ω

   
   
   

   3. 8 Ω

   
   
   

   4. 9 Ω

   
   
   

---

1. View Hint View Answer Discuss in Forum

   For symmetrical network
   A = D = 3
   For bilateral
   AD – BC = 1
   ∴ 9 – C = 1
   ⇒ C = 8 Ω

   Correct Option: B

   For symmetrical network
   A = D = 3
   For bilateral
   AD – BC = 1
   ∴ 9 – C = 1
   ⇒ C = 8 Ω

---

---

113. For the network shown below, Z-parameter will be
     
     
     

1. 1. 
      

   
   
   

   2. 
      

   
   
   

   3. 
      

   
   
   

   4. 

   
   
   

---

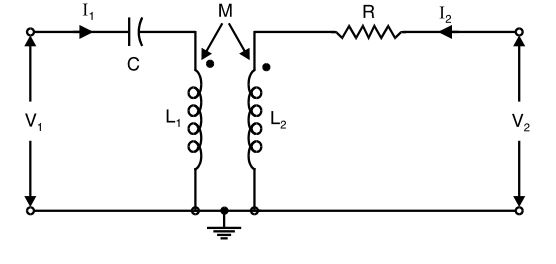
1. View Hint View Answer Discuss in Forum

   Using KVL,
   

   V1(s) =		1	+ sL1		I1(s) + SM.I2(s)
   		sC

   
   and V2 (s) = (R + SL2) I 2 (s) + SM I 1 (s)
   then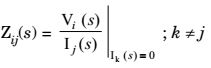
   

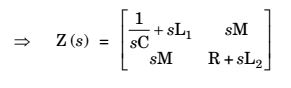
   Correct Option: A

   Using KVL,
   

   V1(s) =		1	+ sL1		I1(s) + SM.I2(s)
   		sC

   
   and V2 (s) = (R + SL2) I 2 (s) + SM I 1 (s)
   then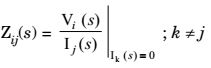
   

---

114. For latice type attenuator shown in the given figure, the characteristic impedance R₀ is
     
     

1. 1. 	R1 + R2
      	2

      
      

   
   
   

   2. 	2R1 + R2
      	R1 + R2

      
      

   
   
   

   3. √R₁ R₂
      

   
   
   

   4. R1 +	R2
      	2

      
      

   
   
   

---

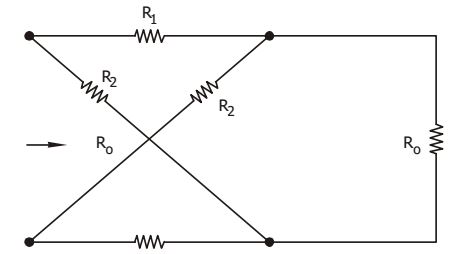
1. View Hint View Answer Discuss in Forum

   Characteristic impedance, R₀ = √R_sc R_oc
   

   Since Rsc = 2	R1 R2	, Roc =	R1 R2
   	R1 + R2		2

   
   ∴ R₀ = √R₁ R₂

   Correct Option: C

   Characteristic impedance, R₀ = √R_sc R_oc
   

   Since Rsc = 2	R1 R2	, Roc =	R1 R2
   	R1 + R2		2

   
   ∴ R₀ = √R₁ R₂

---

---

115. Y parameters of a four terminal block are		4			2		A single element of 1 ohm
     		1			1

     
     is connected across as shown in the given figure. The new Y parameters will be
     
     

1. 1. 	5			1
      	0			2

      
      

   
   
   

   2. 	4			3
      	2			2

      
      

   
   
   

   3. 	3			2
      	1			1

      
      

   
   
   

   4. 	4			2
      	1			1

      
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Y parameter of two networks in parallel are sums of the corresponding Y-parameters.
   
   

   As Y1 =		1			-1
   		-1			1

   
   

   Y2 =		4			2
   		1			1

   
   

   ∴ Y = Y1 + Y2 =		5			1
   		0			2

   Correct Option: A

   Y parameter of two networks in parallel are sums of the corresponding Y-parameters.
   
   

   As Y1 =		1			-1
   		-1			1

   
   

   Y2 =		4			2
   		1			1

   
   

   ∴ Y = Y1 + Y2 =		5			1
   		0			2

---