41. z-matrix for the network shown in the given figure is
    
    
    

1. 1. 
      

   
   
   

   2. 
      

   
   
   

   3. 
      

   
   
   

   4. 

   
   
   

---

1. View Hint View Answer Discuss in Forum

   From the circuit,
   V₁ = I ₁ + (I ₁ + I ₂). 2s
   = (2s + 1) I ₁ + I ₂ . 2s
   

   and V2 =	132	+ (I1 + I2) 2s
   	s

   
   

   = 2s I1 + I2		2s +	3
   			s

   
   
   

   Correct Option: A

   From the circuit,
   V₁ = I ₁ + (I ₁ + I ₂). 2s
   = (2s + 1) I ₁ + I ₂ . 2s
   

   and V2 =	132	+ (I1 + I2) 2s
   	s

   
   

   = 2s I1 + I2		2s +	3
   			s

   
   
   

---

42. Which one of the following parameters does not exist for the two-port network shown in the given figure?
    
    

1. 1. ABCD

   
   
   

   2. y
      

   
   
   

   3. h
      

   
   
   

   4. z

   
   
   

---

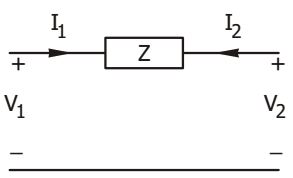
1. View Hint View Answer Discuss in Forum

   Y-parameter =	1		1			-1
   	Z		-1			1

   
   and ∆_y = 0
   Then Z-parameter can not exist.

   Correct Option: C

   Y-parameter =	1		1			-1
   	Z		-1			1

   
   and ∆_y = 0
   Then Z-parameter can not exist.

---

---

43. For the circuit shown in the given figure, when the voltage E is 10 V, the current i is 1 A. If the applied voltage across terminal C-D is 100 V, the short circuit current flowing through the terminal A-B will be
    
    

1. 1. 0.1 A

   
   
   

   2. 1 A

   
   
   

   3. 10 A

   
   
   

   4. 100 A^t

   
   
   

---

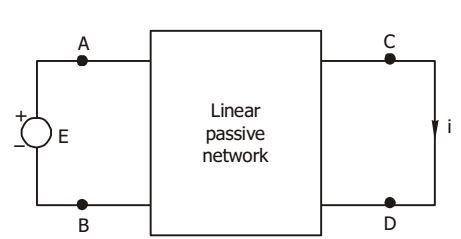
1. View Hint View Answer Discuss in Forum

   Using Y-parameter,
   1₂ = Y₂₁. V_AB + Y₂₂. V_CD
   When V_AB = E = 10_V,
   I ₂ = 1_A, and V_CD = 0
   then Y₂₁ = 0.1
   When port 1 becomes port 2 and vice-versa,
   then 1₂ = Y₂₁. V_CD + Y₂₂. V_AB
   When V_AB = 0, V_CD = 100
   then I₂ = 0.1 × 100 = 10_A
   

   Correct Option: C

   Using Y-parameter,
   1₂ = Y₂₁. V_AB + Y₂₂. V_CD
   When V_AB = E = 10_V,
   I ₂ = 1_A, and V_CD = 0
   then Y₂₁ = 0.1
   When port 1 becomes port 2 and vice-versa,
   then 1₂ = Y₂₁. V_CD + Y₂₂. V_AB
   When V_AB = 0, V_CD = 100
   then I₂ = 0.1 × 100 = 10_A
   

---

44. The driving point impedance Z(s) =	s + 2
    	s + 2

    
    The system is initially at rest. For a voltage signal of unit step, the current i (t) through the impedance Z is given by
    

1. 1. 2 - e^-t
      

   
   
   

   2. 	3	-	1	e-3t
      	2		2

      
      

   
   
   

   3. 	3	-	1	e-2t
      	2		2

      
      

   
   
   

   4. 3 - 2 e^-2t
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   I(s) =	(s + 3)
   	s (s + 2)

   
   

   =	3	-	1	.	1
   	2s		2		s + 2

   
   

   ∴ i(t) =	3	-	1	e-2t
   	2		2

   Correct Option: C

   I(s) =	(s + 3)
   	s (s + 2)

   
   

   =	3	-	1	.	1
   	2s		2		s + 2

   
   

   ∴ i(t) =	3	-	1	e-2t
   	2		2

---

---

45. The driving point impedance of the infinite ladder network shown in the figure is (Given : R₁ = 2 Ω and R₂ = 1.5 Ω)
    
    

1. 1. 3 Ω
      

   
   
   

   2. 3.5 Ω
      

   
   
   

   3. 	3	Ω
      	3.5

      
      

   
   
   

   4. ln		1 +	3		Ω
      			3.5

      
      

   
   
   

---

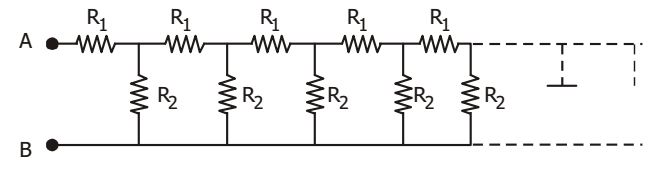
1. View Hint View Answer Discuss in Forum

   Req = R1 +	(R1 + Req) R2
   	R1 + R2 + Req

   
   ⇒ R_eq. R₁ + R_eq. R₂ + R_eq ² = R₁ ² + R₁ R₂ + R_eq R₁ + R₁ R₂ + R_eq . R₂
   ⇒ R_eq = √R₁ ² + 2 R₁ R₂
   = √4 + 2 . 2 . 15
   = √10 = 3.5 Ω

   Correct Option: B

   Req = R1 +	(R1 + Req) R2
   	R1 + R2 + Req

   
   ⇒ R_eq. R₁ + R_eq. R₂ + R_eq ² = R₁ ² + R₁ R₂ + R_eq R₁ + R₁ R₂ + R_eq . R₂
   ⇒ R_eq = √R₁ ² + 2 R₁ R₂
   = √4 + 2 . 2 . 15
   = √10 = 3.5 Ω

---