Electric circuits miscellaneous
- Assuming ideal elements in the circuit shown below, the voltage vab will be

-
View Hint View Answer Discuss in Forum

i = 1 A
∴ Vab – 2i + 5 = 0
or Vab = – 5 + 2i
= – 5 + 2 × 1 = –3Correct Option: A

i = 1 A
∴ Vab – 2i + 5 = 0
or Vab = – 5 + 2i
= – 5 + 2 × 1 = –3
- A capacitor consists of two metal plates each 500 × 500 mm2 and spaced 6 mm apart. The space between the metal plates is filled with a glass plate of 4 mm thickness and a layer of paper of 2 mm thickness. The relative permittivities of the glass and paper are 8 and 2 respectively. Neglecting the fringing effect, the capacitance will be (Given that ε 0 = 8.85 × 10– 12 F/m)
-
View Hint View Answer Discuss in Forum
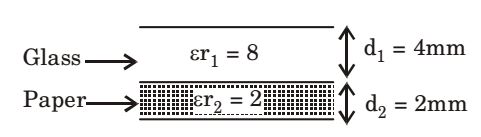
A1 = A2 = 500 × 500 mm2 = 25 × 10 – 2
εr1 = 8, εr2 = 2; d1 = 4, d2 = 2∴ Ceq = C1C2 = Aεr1ε0 . Aεr2ε0 d1 d2 C1 + C2 Aεr1ε0 + Aεr2ε0 d 1 d 2
∴ Ceq = A ε0 εr1 εr2 εr1d2 + εr2d1 = 500 × 500 × 10-6 × 8.85 × 10-12 × 8 × 2 = 1475 μF 8 × 2 + 2 × 4
Correct Option: B

A1 = A2 = 500 × 500 mm2 = 25 × 10 – 2
εr1 = 8, εr2 = 2; d1 = 4, d2 = 2∴ Ceq = C1C2 = Aεr1ε0 . Aεr2ε0 d1 d2 C1 + C2 Aεr1ε0 + Aεr2ε0 d 1 d 2

∴ Ceq = A ε0 εr1 εr2 εr1d2 + εr2d1 = 500 × 500 × 10-6 × 8.85 × 10-12 × 8 × 2 = 1475 μF 8 × 2 + 2 × 4
- A coil of 300 turns is wound on a non-magnetic core having a mean circumference of 300 mm and a cross-sectional area of 300 mm2. The inductance of the coil corresponding to a magnetizing current of 3A will be (Given that μ0 = 4π × 10– 7 H/m)
-
View Hint View Answer Discuss in Forum
Given : n = 300
l = 2πr = 300mm, A = 300mm2 = 300 × 10-6 m2∴ Inductance of coil, L = μ0n2A L = 4π × 10-7 × 300 × 300 × 10-6 = 113.04 μH 300 × 10-3
Correct Option: B
Given : n = 300
l = 2πr = 300mm, A = 300mm2 = 300 × 10-6 m2∴ Inductance of coil, L = μ0n2A L = 4π × 10-7 × 300 × 300 × 10-6 = 113.04 μH 300 × 10-3
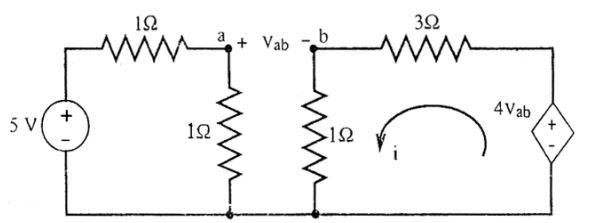
- In the circuit shown in the figure given below, the value of the current i will be given by
-
View Hint View Answer Discuss in Forum
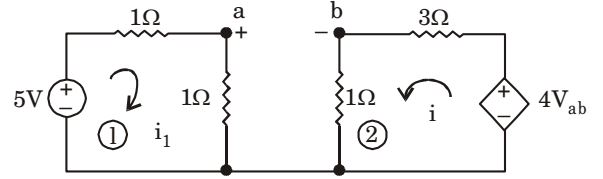
By KVL in loop (1)
5 – 1 × i 1 – 1 × i1 = 0⇒ i1 = 5 = 2.5 A 2
∴ Va = 1 × i1 = 2.5 V ...........(1)
By KVL in loop (2)
4 Vab = 3i + ii = 4Vab = Vab 4
∴ i = Vab ..........(2)
Hence in loop (2)
⇒ Vb = 1 × i
= 1 × Vab
⇒ Vb = Va – Vb⇒ Vb = Va 2
(Putting Va = 2.5 V from (1) we getVb = 2.5 = 1.25 V .......(3) 2
From equations (1) and (3)
i = Vab = (Va – Vb)
= 2.5 – 1.25 = 1.25 A
Correct Option: B

By KVL in loop (1)
5 – 1 × i 1 – 1 × i1 = 0⇒ i1 = 5 = 2.5 A 2
∴ Va = 1 × i1 = 2.5 V ...........(1)
By KVL in loop (2)
4 Vab = 3i + ii = 4Vab = Vab 4
∴ i = Vab ..........(2)
Hence in loop (2)
⇒ Vb = 1 × i
= 1 × Vab
⇒ Vb = Va – Vb⇒ Vb = Va 2
(Putting Va = 2.5 V from (1) we getVb = 2.5 = 1.25 V .......(3) 2
From equations (1) and (3)
i = Vab = (Va – Vb)
= 2.5 – 1.25 = 1.25 A
- Two point charges Q1 = 10 μC and Q2 = 20 μC are placed at coordinates (1, 1, 0) and (– 1, – 1, 0) respect ively. The total electric flux passing through a plane z = 20 will be
-
View Hint View Answer Discuss in Forum
By Gauss’s law,
∮ D .ds = Qend = Ψ
Which states that the “ total flux out of a closed surface is equal to the net charge within the surface”.
Half of the flux will bass through the plane at z = 20 and the other half through the plane at z = – 20Then, Ψ' = Qend = 20 + 10 μc = 15 μ c 2 2 Correct Option: C
By Gauss’s law,
∮ D .ds = Qend = Ψ
Which states that the “ total flux out of a closed surface is equal to the net charge within the surface”.
Half of the flux will bass through the plane at z = 20 and the other half through the plane at z = – 20Then, Ψ' = Qend = 20 + 10 μc = 15 μ c 2 2

