Electric circuits miscellaneous

Electric circuits miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Electric Circuits

Electric circuits miscellaneous
  1. The switch in the circuit has been closed for a long time. It is opened at t = 0. At t = 0+, the current through the 1 μF capacitor is









  1. View Hint View Answer Discuss in Forum

    Circuit at t = 0– (at steady state)

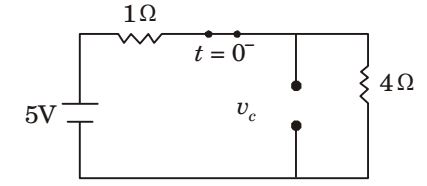
    Initial voltage, Vc (0–) =
    4
    		 × 5 = 4 V
    1 + 4

    Circuit at t = 0+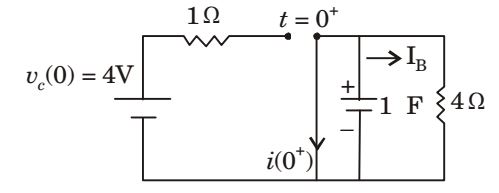

    ic(0+) = IB =
    4
    		 = 1 amp
    4

    i =
    Vc
    		e-t / RC
    R

    Correct Option: B

    Circuit at t = 0– (at steady state)

    Initial voltage, Vc (0–) =
    4
    		 × 5 = 4 V
    1 + 4

    Circuit at t = 0+

    ic(0+) = IB =
    4
    		 = 1 amp
    4

    i =
    Vc
    		e-t / RC
    R

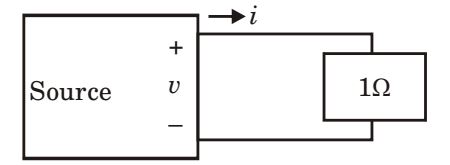
  1. As shown in the figure given below, a 1Ω resistance is connected across a source that has a load line v + i = 100. The current through the resistance is









  1. View Hint View Answer Discuss in Forum


    Load line : v + i = 100
    From figure, we have
    v = 1 × i = i
    ⇒ v = i
    ∴ i + i = 100
    ⇒ i = 50 A

    Correct Option: B


    Load line : v + i = 100
    From figure, we have
    v = 1 × i = i
    ⇒ v = i
    ∴ i + i = 100
    ⇒ i = 50 A

  1. A wattmeter is connected as shown in the figure given below. The wattmeter reads









  1. View Hint View Answer Discuss in Forum


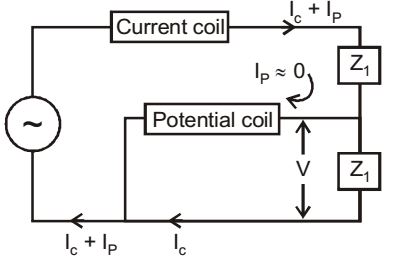
    Since potential coil draws negligible current, IP ≈ 0 and current through Z1 and Z2 will be same.
    Then, wattmeter will read power consumed by Z2, P = IC .V where V is potential across Z2.

    Correct Option: D


    Since potential coil draws negligible current, IP ≈ 0 and current through Z1 and Z2 will be same.
    Then, wattmeter will read power consumed by Z2, P = IC .V where V is potential across Z2.

  1. If 12 Ω resistor draws a current of 1 A as shown in the figure given below, the value of resistance R is









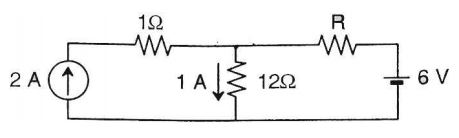
  1. View Hint View Answer Discuss in Forum


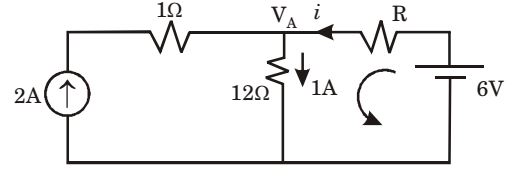
    VA = 12
    i = 1 – 2 = – 1 amp.
    By KVL, 6 – iR – 12 × 1 = 0
    ⇒ iR = – 6

    ⇒ R =
    -6
    		 = 6 Ω
    (-1)

    Correct Option: B


    VA = 12
    i = 1 – 2 = – 1 amp.
    By KVL, 6 – iR – 12 × 1 = 0
    ⇒ iR = – 6

    ⇒ R =
    -6
    		 = 6 Ω
    (-1)

  1. The two-port network P shown in the figure has ports 1 and 2, denoted by terminals (a, b) and (c, d) respectively. It has an impedance matrix Z with parameters denoted by zij . A 1 Ω resistor is connected in series with the network at port 1 as shown in the figure. The impedance matrix of the modified two-port networ k (shown as a dashed box) is








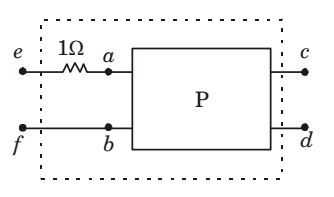
  1. View Hint View Answer Discuss in Forum

    Case 1

    V1 = Z11 i 1 + Z12 i 2
    V2 = Z21 i 1 + Z22 i2
    Case 2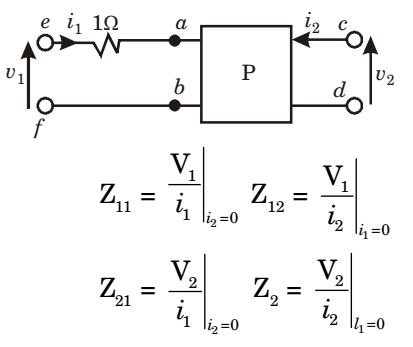

    Equivalent circuits
    For case 1 : Z11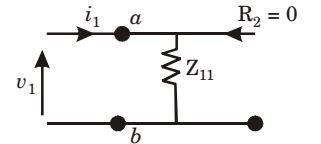

    For case 2 :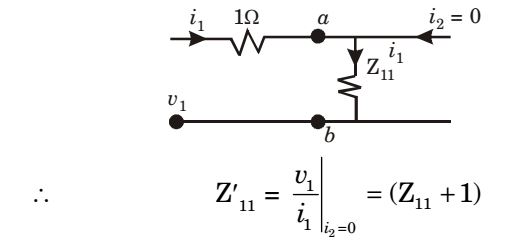

    For case 1 :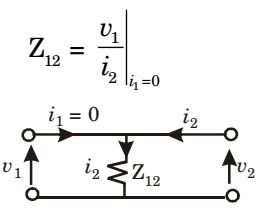

    For case 2 :

    Z21 for case 1 :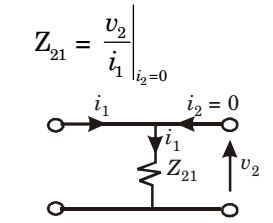

    For case 2 :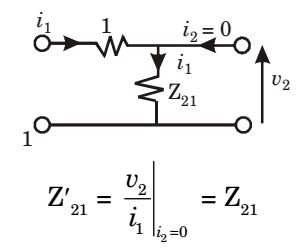

    Z22 for case 1 :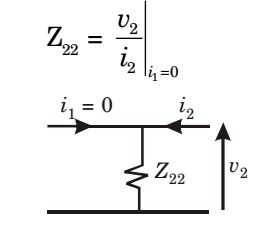

    For case 2 :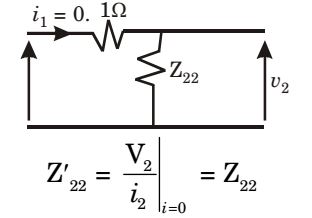

    ∴ New impedance matrix,

    Z' = Z11 + 1
    Z12
    Z21Z22

    Correct Option: C

    Case 1

    V1 = Z11 i 1 + Z12 i 2
    V2 = Z21 i 1 + Z22 i2
    Case 2

    Equivalent circuits
    For case 1 : Z11

    For case 2 :

    For case 1 :

    For case 2 :

    Z21 for case 1 :

    For case 2 :

    Z22 for case 1 :

    For case 2 :

    ∴ New impedance matrix,

    Z' = Z11 + 1
    Z12
    Z21Z22