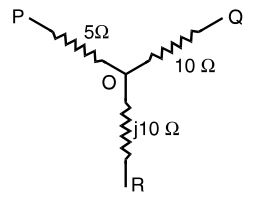
21. In the delta equivalent of the given star connected circuit, Z_OR is equal to
    
    

1. 1. 40 Ω

   
   
   

   2. (20 + j10) Ω

   
   
   

   3. 5 + j	10	Ω
      	3

   
   
   

   4. (10 + j30) Ω

   
   
   

---

1. View Hint View Answer Discuss in Forum

   ZQR =	5 × 10 + 10 × j10 + j10 × 5	= (10 + j30 ) Ω
   	5

   Correct Option: D

   ZQR =	5 × 10 + 10 × j10 + j10 × 5	= (10 + j30 ) Ω
   	5

---

22. A delta connected network with Y-equivalent is shown below.
    
    The resistances R₁, R₂, R₃ (in ohms) are respectively
    

1. 1. 1.5, 3 and 9

   
   
   

   2. 3, 9 and 1.5

   
   
   

   3. 9, 3 and 1.5

   
   
   

   4. 3, 1.5 and 9

   
   
   

---

1. View Hint View Answer Discuss in Forum

   R1 =	Rab Rac	=	150	= 3
   	Rab + Rac + Rbc		50

   
   

   R2 =	Rab Rac	=	5 × 25	= 1.5
   	Rab + Rac + Rbc		50

   
   

   R3 =	30 × 15	= 9
   	50

   
   

   Correct Option: D

   R1 =	Rab Rac	=	150	= 3
   	Rab + Rac + Rbc		50

   
   

   R2 =	Rab Rac	=	5 × 25	= 1.5
   	Rab + Rac + Rbc		50

   
   

   R3 =	30 × 15	= 9
   	50

   
   
   

---

---

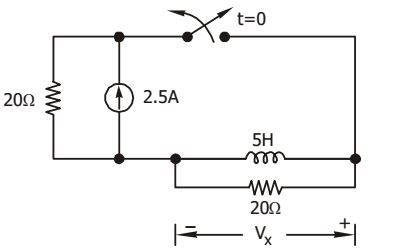
23. In the given figure, the switch was closed for a long time before opening at t = 0. The voltage V_x at t = 0⁺ is
    
    

1. 1. 25 V

   
   
   

   2. 50 V

   
   
   

   3. – 50 V

   
   
   

   4. 0 V

   
   
   

---

1. View Hint View Answer Discuss in Forum

   At t = 0⁺ , the circuit will be as shown below.
   
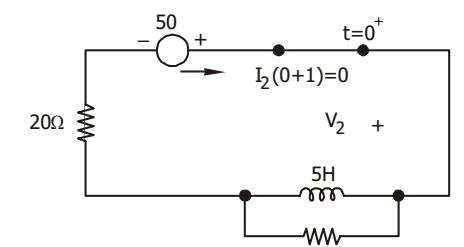
   I _L (0⁺) = 0
   Then V_i = – 50 V

   Correct Option: C

   At t = 0⁺ , the circuit will be as shown below.
   
   I _L (0⁺) = 0
   Then V_i = – 50 V

---

24. In a passive two-port network, the open-circuit impedance matrix is		10			2
    		5			2

    
    If input port is interchanged with the output port, then open-circuit impedance matrix will be
    

1. 1. 	10			2
      	5			2

      
      

   
   
   

   2. 	5			2
      	2			10

      
      

   
   
   

   3. 	5			10
      	2			2

      
      

   
   
   

   4. 	2			5
      	10			2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   The port-equations are
   V₁ = 10 I ₁ + 2I ₂ ....(i)
   V₂ = 2I ₁ + 5 I₂ ....(ii)
   Rewriting equations (i) and (ii) as
   V₂ = 5 I₂ + 2I₁ ....(iii)
   V₁ = 2 I₂ + 10 I₁ ....(iv)
   Writing in matrix form
   

   
   

   		V2		=		5			2			I2
   		V1				2			10			I1

   
   

   Correct Option: B

   The port-equations are
   V₁ = 10 I ₁ + 2I ₂ ....(i)
   V₂ = 2I ₁ + 5 I₂ ....(ii)
   Rewriting equations (i) and (ii) as
   V₂ = 5 I₂ + 2I₁ ....(iii)
   V₁ = 2 I₂ + 10 I₁ ....(iv)
   Writing in matrix form
   

   
   

   		V2		=		5			2			I2
   		V1				2			10			I1

   
   

---

---

25. An ideal transformer has turns ratio of 2 : 1. Considering high voltage side as port 1 and low voltage side as port 2, then transmission line parameters of transformer will be
    

1. 1. 	0			-2
      	0.5			0

      
      

   
   
   

   2. 	-2			0
      	0			-0.5

      
      

   
   
   

   3. 	2			0
      	0			-0.5

      
      

   
   
   

   4. 	0.5			0
      	0			2

      
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   	V1	=	I1	=	N1	=	2
   	V2		I2		N2		1

   
   ⇒ V₁ = 2V₂
   I ₁ = 0.5 I₂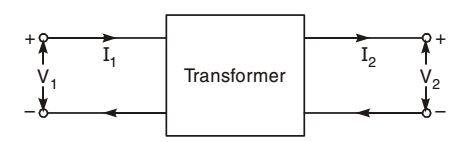
   
   In matrix form,
   
   

   		V1		=		2			0			V2
   		I1				0			-0.5			I2

   
   

   Correct Option: C

   	V1	=	I1	=	N1	=	2
   	V2		I2		N2		1

   
   ⇒ V₁ = 2V₂
   I ₁ = 0.5 I₂
   
   In matrix form,
   
   

   		V1		=		2			0			V2
   		I1				0			-0.5			I2

   
   

---