106. In respect of the 2-port network shown in the given figure, admittance parameters are :
     Y₁₁ = 8 mho, Y₁₂ = Y₂₁ = – 6 mho and Y₂₂ = 6 mho. The values of Y_A, Y_B and Y_C (in units of mho) will be respectively
     

1. 1. 2, 6 and – 6

   
   
   

   2. 2, 6 and 0

   
   
   

   3. 2, 0 and 6

   
   
   

   4. 2, 6 and 8

   
   
   

---

1. View Hint View Answer Discuss in Forum

   From the circuit, I₁ = (V₁ – V₂) Y_C + V₁ .Y_A
   = – V₁ (Y_A + Y_C) – V₂. Y_C ....(i)
   I₂ = V₁Y_C + V₂ (Y_B + Y_C) ...(ii)
   Y_A + Y_C = Y₁₁ = 8 Ω
   Y_C = Y₁₂ = – Y₂₁ = 6 Ω
   Y_B + Y_C = Y₂₂ = 6 Ω
   ∴ Y_A = 2, Y_B = 0, Y_C = 6 Ω

   Correct Option: C

   From the circuit, I₁ = (V₁ – V₂) Y_C + V₁ .Y_A
   = – V₁ (Y_A + Y_C) – V₂. Y_C ....(i)
   I₂ = V₁Y_C + V₂ (Y_B + Y_C) ...(ii)
   Y_A + Y_C = Y₁₁ = 8 Ω
   Y_C = Y₁₂ = – Y₂₁ = 6 Ω
   Y_B + Y_C = Y₂₂ = 6 Ω
   ∴ Y_A = 2, Y_B = 0, Y_C = 6 Ω

---

107. For the given network, [y] is equal to
     
     
     

1. 1. 
      

   
   
   

   2. 
      

   
   
   

   3. 
      

   
   
   

   4. 

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

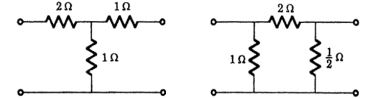
   [ za ] =		3			1
   		1			2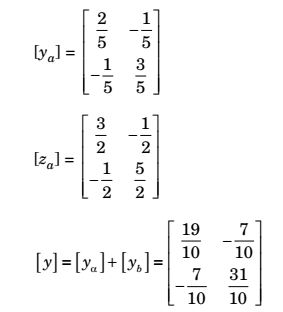

   
   

   Correct Option: B

   
   

   [ za ] =		3			1
   		1			2

   
   

---

---

108. V-I relation for the network shown in the given box is V = 4I – 9. I f now a resistor R = 2 Ω is connected across it, then value of I will be
     
     

1. 1. – 4.5 A

   
   
   

   2. – 1.5 A

   
   
   

   3. 1.5 A

   
   
   

   4. 4.5 A

   
   
   

---

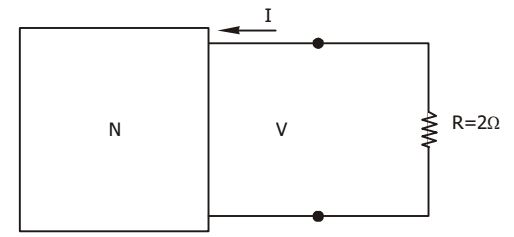
1. View Hint View Answer Discuss in Forum

   V = 4I – 9 = – IR
   ⇒ 4I – 9 = – 2I
   ⇒ I = 1.5 A
   

   Correct Option: C

   V = 4I – 9 = – IR
   ⇒ 4I – 9 = – 2I
   ⇒ I = 1.5 A
   

---

109. Initially, the circuit shown in the given figure was relaxed. If switch is closed at t = 0, then
     

     values of i(0+),	di	(0+) and	d2i	(0+) will respectively be
     	dt		dt2

     
     
     

1. 1. 0, 10 and – 100

   
   
   

   2. 0, 10 and 100

   
   
   

   3. 10, 100 and 0

   
   
   

   4. 100, 0 and 10

   
   
   

---

1. View Hint View Answer Discuss in Forum

   By KVL equation
   

   10 = i R +	L di	+ Vc ......(i)
   	dt

   
   At t = 0⁺, t = 0 and V_c = 0 (short-circuited)
   
   Differentiating equation (i), we have
   

   10 =	di	R +	Ld2i	+	dvc
   	dt		dt2		dt

   
   

   ⇒	Ld2i	= -	di	R ......		as	dVc	=	i	= 0
   	dt2		dt				dt		C

   
   

   ⇒	Ld2i	= - 10 × 10 = - 100
   	dt2

   Correct Option: A

   By KVL equation
   

   10 = i R +	L di	+ Vc ......(i)
   	dt

   
   At t = 0⁺, t = 0 and V_c = 0 (short-circuited)
   
   Differentiating equation (i), we have
   

   10 =	di	R +	Ld2i	+	dvc
   	dt		dt2		dt

   
   

   ⇒	Ld2i	= -	di	R ......		as	dVc	=	i	= 0
   	dt2		dt				dt		C

   
   

   ⇒	Ld2i	= - 10 × 10 = - 100
   	dt2

---

---

110. An impedance match is desired at the 1 – 1 port of the two-port network shown in the given figure. The match will be obtained when z_g equals
     
     

1. 1. z₁ + z₃
      

   
   
   

   2. z1 +	z3(z2 + zL)
      	2

      
      

   
   
   

   3. 	z1(z2 + z3)
      	z1 + z2 + z3

      
      

   
   
   

   4. none of these
      

   
   
   

---

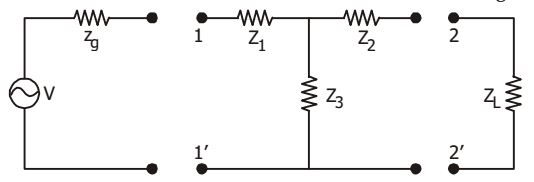
1. View Hint View Answer Discuss in Forum

   Equivalent resistance looking right through terminal 11',
   

   Zeq =	(Z2 + ZL)Z3	+ Z1
   	Z2 + Z3 + ZL

   
   For impedance matching,
   Z_eq= Z_g
   

   Correct Option: B

   Equivalent resistance looking right through terminal 11',
   

   Zeq =	(Z2 + ZL)Z3	+ Z1
   	Z2 + Z3 + ZL

   
   For impedance matching,
   Z_eq= Z_g
   

---