96. For the circuit shown in the given figure, when the voltage E is 10 V, the current i is 1 A. If the applied voltage across terminal C-D is 100 V, the short circuit current flowing through the terminal A-B will be
    
    

1. 1. 0.1 A

   
   
   

   2. 1 A

   
   
   

   3. 10 A

   
   
   

   4. 100 A^t

   
   
   

---

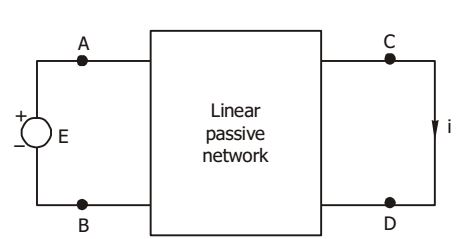
1. View Hint View Answer Discuss in Forum

   Using Y-parameter,
   1₂ = Y₂₁. V_AB + Y₂₂. V_CD
   When V_AB = E = 10_V,
   I ₂ = 1_A, and V_CD = 0
   then Y₂₁ = 0.1
   When port 1 becomes port 2 and vice-versa,
   then 1₂ = Y₂₁. V_CD + Y₂₂. V_AB
   When V_AB = 0, V_CD = 100
   then I₂ = 0.1 × 100 = 10_A
   

   Correct Option: C

   Using Y-parameter,
   1₂ = Y₂₁. V_AB + Y₂₂. V_CD
   When V_AB = E = 10_V,
   I ₂ = 1_A, and V_CD = 0
   then Y₂₁ = 0.1
   When port 1 becomes port 2 and vice-versa,
   then 1₂ = Y₂₁. V_CD + Y₂₂. V_AB
   When V_AB = 0, V_CD = 100
   then I₂ = 0.1 × 100 = 10_A
   

---

97. The driving point impedance Z(s) =	s + 2
    	s + 2

    
    The system is initially at rest. For a voltage signal of unit step, the current i (t) through the impedance Z is given by
    

1. 1. 2 - e^-t
      

   
   
   

   2. 	3	-	1	e-3t
      	2		2

      
      

   
   
   

   3. 	3	-	1	e-2t
      	2		2

      
      

   
   
   

   4. 3 - 2 e^-2t
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   I(s) =	(s + 3)
   	s (s + 2)

   
   

   =	3	-	1	.	1
   	2s		2		s + 2

   
   

   ∴ i(t) =	3	-	1	e-2t
   	2		2

   Correct Option: C

   I(s) =	(s + 3)
   	s (s + 2)

   
   

   =	3	-	1	.	1
   	2s		2		s + 2

   
   

   ∴ i(t) =	3	-	1	e-2t
   	2		2

---

---

98. The driving point impedance of the infinite ladder network shown in the figure is (Given : R₁ = 2 Ω and R₂ = 1.5 Ω)
    
    

1. 1. 3 Ω
      

   
   
   

   2. 3.5 Ω
      

   
   
   

   3. 	3	Ω
      	3.5

      
      

   
   
   

   4. ln		1 +	3		Ω
      			3.5

      
      

   
   
   

---

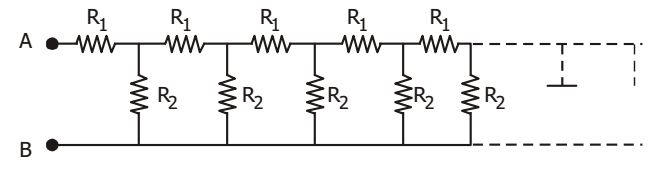
1. View Hint View Answer Discuss in Forum

   Req = R1 +	(R1 + Req) R2
   	R1 + R2 + Req

   
   ⇒ R_eq. R₁ + R_eq. R₂ + R_eq ² = R₁ ² + R₁ R₂ + R_eq R₁ + R₁ R₂ + R_eq . R₂
   ⇒ R_eq = √R₁ ² + 2 R₁ R₂
   = √4 + 2 . 2 . 15
   = √10 = 3.5 Ω

   Correct Option: B

   Req = R1 +	(R1 + Req) R2
   	R1 + R2 + Req

   
   ⇒ R_eq. R₁ + R_eq. R₂ + R_eq ² = R₁ ² + R₁ R₂ + R_eq R₁ + R₁ R₂ + R_eq . R₂
   ⇒ R_eq = √R₁ ² + 2 R₁ R₂
   = √4 + 2 . 2 . 15
   = √10 = 3.5 Ω

---

99. With the usual notations, a two-port resistive network satisfies the condition A = D =	3	B =	4	C
    	2		3

    
    z₁₁ of the network is
    

1. 1. 	5
      	3

      
      

   
   
   

   2. 	4
      	3

      
      

   
   
   

   3. 	4
      	3

      
      

   
   
   

   4. 	1
      	3

      
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Z11 =	A	=	4
   	C		4

   
   

   Correct Option: B

   Z11 =	A	=	4
   	C		4

   
   

---

---

100. A two-port network is defined by the relations I₁ = 2V₁ + V₂, I₂ = 2V₁ + 3V₂ Then z₁₂ is
     

1. 1. – 2 Ω

   
   
   

   2. – 1 Ω

   
   
   

   3. -	1	Ω
      	2

      
      

   
   
   

   4. 	1	Ω
      	4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   From the equations,
   

   I1 = 2V1 +	(I2 - 2V1)
   	3

   
   

   ⇒ V1 = 3I1 -	I2
   	4

   
   

   ∴ Z12 =	1	Ω
   	4

   
   

   Correct Option: D

   From the equations,
   

   I1 = 2V1 +	(I2 - 2V1)
   	3

   
   

   ⇒ V1 = 3I1 -	I2
   	4

   
   

   ∴ Z12 =	1	Ω
   	4

   
   

---