Electric circuits miscellaneous Easy Questions and Answers | Page - 36

Electric circuits miscellaneous

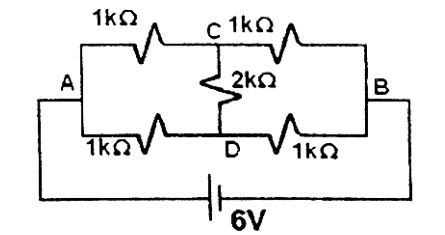
The current through the 2 kΩ resistance in the circuit shown below is

1. 0 mA
1. 1 mA
1. 2 mA
1. 6 mA

View Hint View Answer Discuss in Forum

This is a balance Wheatstone bridge.

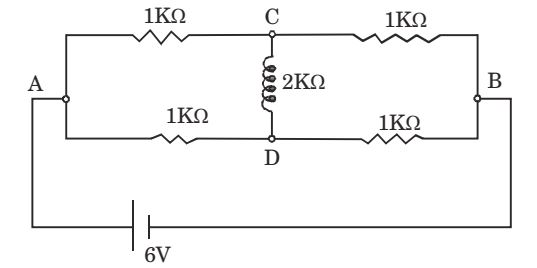
∴ V_CD = 0 (V_C = V_D)
∴ i _CD = 0

Correct Option: A

This is a balance Wheatstone bridge.

∴ V_CD = 0 (V_C = V_D)
∴ i _CD = 0

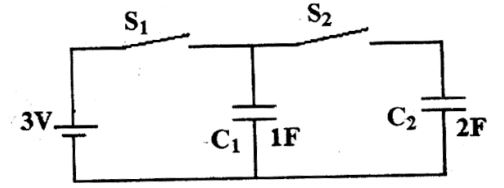
In the figure shown below, all elements used are ideal. For time t < 0,S₁ remained closed and S₂ open. At t = 0, S₁ is opened and S₂ is closed. If the voltage V_c2 across the capacitor C_c at t = 0 is zero, the voltage across the capacitor combination at t = 0⁺ will be

1. 1 V
1. 2 V
1. 1.5 V
1. 3 V

View Hint View Answer Discuss in Forum

For t < 0, s₁ in closed and s₂ open

Q_c₁ = C₁ V = 3 C
Q_c₂ = 0
At t = 0, S₁ is opened and S₂ is closed.
Now, let Q ' _c₁ and Q ' _c₂ is the change stored after redistribution
then, Q ' _c₁ + Q ' _c₂ = Q _c₁ + Q _c₂ = 3C ...(A)
Q ' _c₁ = Q ' _c₂
c₁ c₂

[Equal potential across C₁ and C₂].
⇒ Q ' _c₁ = Q ' _c₂ .......(B)
1 2

By equation (A) and equation (B),
Q '_c₁ = 1C as Q' _c₂ = 2C
and voltage across capacitor combination is,
= Q'_c₁ = 1 volt
C₁

Correct Option: D

For t < 0, s₁ in closed and s₂ open

Q_c₁ = C₁ V = 3 C
Q_c₂ = 0
At t = 0, S₁ is opened and S₂ is closed.
Now, let Q ' _c₁ and Q ' _c₂ is the change stored after redistribution
then, Q ' _c₁ + Q ' _c₂ = Q _c₁ + Q _c₂ = 3C ...(A)
Q ' _c₁ = Q ' _c₂
c₁ c₂

[Equal potential across C₁ and C₂].
⇒ Q ' _c₁ = Q ' _c₂ .......(B)
1 2

By equation (A) and equation (B),
Q '_c₁ = 1C as Q' _c₂ = 2C
and voltage across capacitor combination is,
= Q'_c₁ = 1 volt
C₁

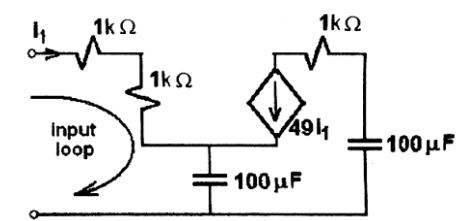
The equivalent capacitance of the input loop of the circuit shown below is

1. 2μ F
1. 100μF
1. 200μF
1. 4μF

View Hint View Answer Discuss in Forum

We know, Q = CV
But voltage across capacitor is constant.
C ∝ Q
⇒ C ∝ i
∴ C_total ∝ (i₁ + i₂)
C_in ∝ l_i
∴ C_in = i_s
(i₁ + i₂)

C_total = i₁ (100 μF)
(i₁ + 49i₁)

= i₁ (100 μF) = 2μF
50i₁

Alternately
V_in = 2RI₁ + 1 50
jωC

I₁ = 2RI₁ + 1 I₁
jωC_eq

∴ C_eq = C = 2 μF
50

Correct Option: A

We know, Q = CV
But voltage across capacitor is constant.
C ∝ Q
⇒ C ∝ i
∴ C_total ∝ (i₁ + i₂)
C_in ∝ l_i
∴ C_in = i_s
(i₁ + i₂)

C_total = i₁ (100 μF)
(i₁ + 49i₁)

= i₁ (100 μF) = 2μF
50i₁

Alternately
V_in = 2RI₁ + 1 50
jωC

I₁ = 2RI₁ + 1 I₁
jωC_eq

∴ C_eq = C = 2 μF
50

For the graph shown in figure set of twigs is

1. e f
1. a b e f
1. c d e
1. none of these

View Hint View Answer Discuss in Forum

Twigs are branches of the tree.
From the figure c d e is tree of graph.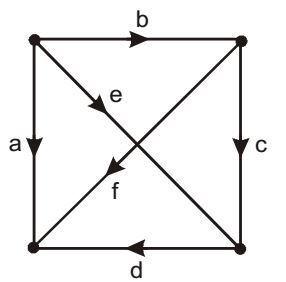

Correct Option: C

Twigs are branches of the tree.
From the figure c d e is tree of graph.

For the circuit shown in the given figure, when the switch is at position A, the current i(t) = I sin (ωt + 30°) A. When switch is moved to position B at time t = 0, the power dissipated at the switching inst ant in the resistor R remains unchanged The value of I and the element X would respectively, be

1. 1 A and resistor
1. 2 A and capacitor
1. 3 A and resistor
1. 4 A and capacitor

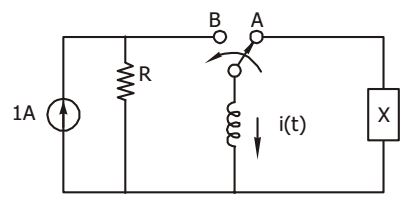
View Hint View Answer Discuss in Forum

NA

Correct Option: D

NA