Electric circuits miscellaneous

Electric circuits miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Electric Circuits

Electric circuits miscellaneous
  1. The two electric sub-networks N1 and N2 are connected through three resistors as shown in the figure below. The voltage across 5 Ω resistor and 1 Ω resistor are given to be 10V and 5V respectively. Then voltage across 15 Ω resistor is








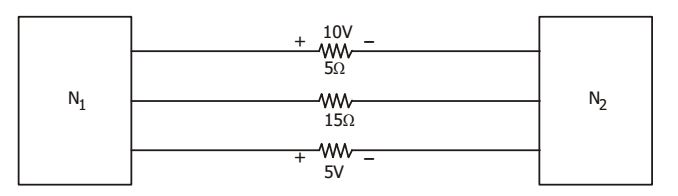
  1. View Hint View Answer Discuss in Forum

    By KCL, if we take a cutset along all three branches, then total current at the junction is zero.
    i.e. I 1 + I 2 + I 3 = 0

    ⇒
    10
    		 + I2 +
    5
    		 = 0
    51

    ⇒ I2 = 7A
    and V = – 105 V.

    Correct Option: A

    By KCL, if we take a cutset along all three branches, then total current at the junction is zero.
    i.e. I 1 + I 2 + I 3 = 0

    ⇒
    10
    		 + I2 +
    5
    		 = 0
    51

    ⇒ I2 = 7A
    and V = – 105 V.

  1. In the given circuit, voltages V1 and V2 respectively are









  1. View Hint View Answer Discuss in Forum

    I1 = 10 × 10– 3 V1 – 5 × 10– 3V2
    100 = 25I1 + V1
    100 – V1 = 0.25V1 – 0.125 V2
    ⇒ 800 = 10 V2....(i)
    I 2 = 50 × 10– 3 V1 + 20 × 10– 3V2
    V2 = – 100 I2
    ∴ V2 = 5V1 – 2V2
    ⇒ 3V2 + 5V1 = 0 ....(ii)
    Solving equations (i) and (ii), we get
    V1 = 68.6 V, and V2 = – 114.3 V

    Correct Option: B

    I1 = 10 × 10– 3 V1 – 5 × 10– 3V2
    100 = 25I1 + V1
    100 – V1 = 0.25V1 – 0.125 V2
    ⇒ 800 = 10 V2....(i)
    I 2 = 50 × 10– 3 V1 + 20 × 10– 3V2
    V2 = – 100 I2
    ∴ V2 = 5V1 – 2V2
    ⇒ 3V2 + 5V1 = 0 ....(ii)
    Solving equations (i) and (ii), we get
    V1 = 68.6 V, and V2 = – 114.3 V

  1. A T-network is shown in the given figure. Its Y matrix will be (units in siemens)










  1. View Hint View Answer Discuss in Forum

    NA

    Correct Option: C

    NA

  1. The driving-point impedance of a one-port reactive network is given by








  1. View Hint View Answer Discuss in Forum

    For an L– C network, driving-point impedance function poles and zeros should alternate. This is satisfied by the function at (b) alone.

    Correct Option: B

    For an L– C network, driving-point impedance function poles and zeros should alternate. This is satisfied by the function at (b) alone.

  1. In the circuit shown in the given figure, G12 =
    V2
    		 = ?
    V1










  1. View Hint View Answer Discuss in Forum

    I2 = y21V1 + y22V2
    I2 = – V2 YL
    y21V1 + (y22 + YL )V2 = 0

    ∴
    V2
    		 =
    -y21
    V1(y22 + yL)

    Correct Option: B

    I2 = y21V1 + y22V2
    I2 = – V2 YL
    y21V1 + (y22 + YL )V2 = 0

    ∴
    V2
    		 =
    -y21
    V1(y22 + yL)