56. In the circuit shown, the value at I is _______ A
    
    

1. 1. 0

   
   
   

   2. 1

   
   
   

   3. 2

   
   
   

   4. 3

   
   
   

---

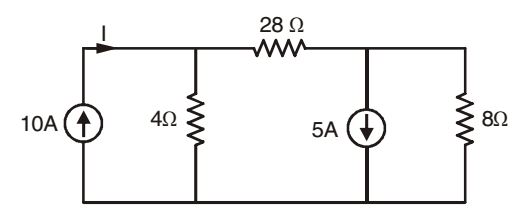
1. View Hint View Answer Discuss in Forum

   Converting current source into voltage source, I =	80	= 2 A
   	40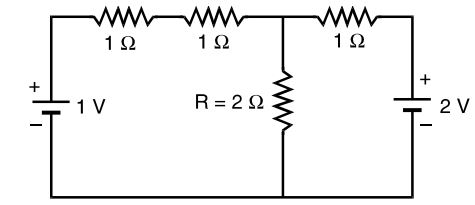

   
   
   

   Correct Option: C

   Converting current source into voltage source, I =	80	= 2 A
   	40

   
   
   

---

57. In the figure shown if we connect a source of 2 V with internal resistance of 1 Ω at A' A with positive terminal at A', then the current through R is _________ .
    

1. 1. 51.125 A

   
   
   

   2. 10.125 A

   
   
   

   3. 0.625 A

   
   
   

   4. 10.65 A

   
   
   

---

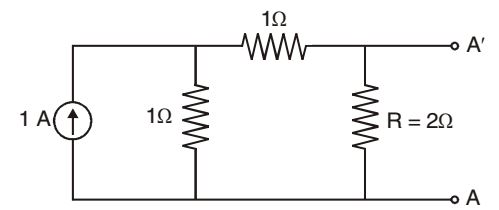
1. View Hint View Answer Discuss in Forum

   
   After converting current source into voltage source, the circuit becomes as given below.
   Using superposition principle,
   

   current through ,R =	1	+	1	= 0.625 A
   	8		2

   
   

   Correct Option: C

   
   After converting current source into voltage source, the circuit becomes as given below.
   Using superposition principle,
   

   current through ,R =	1	+	1	= 0.625 A
   	8		2

   
   

---

---

58. A series R-L-C circuit has R = 50 Ω , L = 100 F and C = 1 µF. The lower half power frequency of the circuit is _________ kHz

1. 1. 3.055 k Hz.

   
   
   

   2. 1.01 k Hz.

   
   
   

   3. 14.054 k Hz.

   
   
   

   4. None of the above

   
   
   

---

1. View Hint View Answer Discuss in Forum

   For series RLC circuit, at lower half power frequency
   

   ω1L -	1	= - R
   	ω1C

   
   

   ⇒ 2πf1 × 100 × 10-6 -	1	= - 50
   	2πf1 × 1 × 10-6

   
   ⇒ f₁ = 3.055 k H z.

   Correct Option: A

   For series RLC circuit, at lower half power frequency
   

   ω1L -	1	= - R
   	ω1C

   
   

   ⇒ 2πf1 × 100 × 10-6 -	1	= - 50
   	2πf1 × 1 × 10-6

   
   ⇒ f₁ = 3.055 k H z.

---

59. In the circuit of the given figure, the magnitudes of V_L and V_C are twice that of V_R. The inductance of the coil is ________ mH.
    

1. 1. 31.8 mH

   
   
   

   2. 11.3 mH

   
   
   

   3. 61.1 mH

   
   
   

   4. 21.8 mH

   
   
   

---

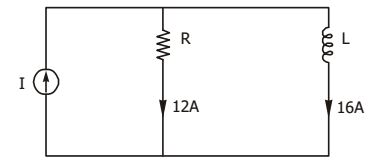
1. View Hint View Answer Discuss in Forum

   Since V_L = V_C , then circuit is in resonance and current,
   

   L =	5	=	5	= 1 A
   	R		5

   
   Voltage, V_L = 2V_R = 10
   ∴ ω L = 10
   

   ⇒ L =	10	=	10	=	10	= 31.8 mH
   	ω		2πf R		2π × 50

   
   

   Correct Option: A

   Since V_L = V_C , then circuit is in resonance and current,
   

   L =	5	=	5	= 1 A
   	R		5

   
   Voltage, V_L = 2V_R = 10
   ∴ ω L = 10
   

   ⇒ L =	10	=	10	=	10	= 31.8 mH
   	ω		2πf R		2π × 50

   
   

---

---

60. In the circuit shown in the given figure, the current supplied by t he sinusoidal cur rent source I is __________ A
    

1. 1. 1 A

   
   
   

   2. 5 A

   
   
   

   3. 10 A

   
   
   

   4. 20 A

   
   
   

---

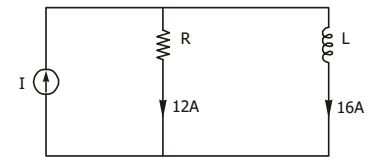
1. View Hint View Answer Discuss in Forum

   I = √I_R² + I_L²
   (both I_R and I_L in quadrature)
   = √12² + 16² = 20 A

   Correct Option: D

   I = √I_R² + I_L²
   (both I_R and I_L in quadrature)
   = √12² + 16² = 20 A

---