Speed, Time and Distance
- A man completes 30 km of a journey at 6 km/h and the remaining 40 km of the journey in 5 h. Find the average speed for the whole journey.
-
View Hint View Answer Discuss in Forum
Total distance = 30 + 40 = 70 km
Total time taken = (30/6) + 5 = 10 hCorrect Option: B
Total distance = 30 + 40 = 70 km
Total time taken = (30/6) + 5 = 10 h
∴ Required average speed = 70/10 = 7 km/h
- A train after travelling 100 kms from P meets with an accident and then proceeds
at the terminus Q 90 minutes late. Had the accident occurred 60 kms further on, it would have reached 15 minutes sooner. Find the original speed of the train and the distance PQ.at 3 th of its original speed and arrives 4
-
View Hint View Answer Discuss in Forum
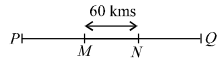
Let P be the starting point, Q the terminus, M and N the places where accidents occur.
At (3/4)th of the original speed, the train will take 4/3 of its usual time to cover the same distance i.e., (1/3)rd more than the usual time.
(1/3)rd of the usual time to travel a distance of 60 kms between MN = 15 min.
∴ Usual time to travel 60 kms= 15 × 3 = 45 min. = 3 hr. 4
∴ Usual speed of the train per hour= 60 × 4 = 80 km per hr. 3
Usual time taken to travel MQ = 90 × 3= 270 min. or 9 hrs. 2 = 80 × 9 = 360 km. 2
Therefore, the total distance PQ
= PM + MQ
= 100 + 360 = 460 kms.Correct Option: C

Let P be the starting point, Q the terminus, M and N the places where accidents occur.
At (3/4)th of the original speed, the train will take 4/3 of its usual time to cover the same distance i.e., (1/3)rd more than the usual time.
(1/3)rd of the usual time to travel a distance of 60 kms between MN = 15 min.
∴ Usual time to travel 60 kms= 15 × 3 = 45 min. = 3 hr. 4
∴ Usual speed of the train per hour= 60 × 4 = 80 km per hr. 3
Usual time taken to travel MQ = 90 × 3= 270 min. or 9 hrs. 2 = 80 × 9 = 360 km. 2
Therefore, the total distance PQ
= PM + MQ
= 100 + 360 = 460 kms.
- A hare, pursued by a grey hound is 50 of her own leaps before him. While the hare takes 4 leaps, the grey hound takes 3 leaps. In one leap, the hare goes 1.75 metres and the grey hound 2.75 metres. In how many leaps, will the grey hound overtake the hare?
-
View Hint View Answer Discuss in Forum
Grey hound and hare make 3 leaps and 4 leaps respectively. This happens at the same time.
The hare goes 1.75 metres in 1 leap.
∴ Distance covered by hare in 4 leaps = 4 × 1.75 = 7 metres
The grey hound goes 2.75 metres in one leap.
∴ Distance covered by it in 3
leaps
= 3 × 2.75 = 8.25 metres
Distance gained by grey hound in 3 leaps = (8.25 − 7)
= 1.25 metres
Distance covered by hare in 50 leaps = 50 × 1.75 metres
= 87.5 metres
Now, 1.25 metres is gained by grey hound in 3 leaps
∴ 87.5 metres is gained in3 × 87.5 = 210 leaps. 1.25 Correct Option: A
Grey hound and hare make 3 leaps and 4 leaps respectively. This happens at the same time.
The hare goes 1.75 metres in 1 leap.
∴ Distance covered by hare in 4 leaps = 4 × 1.75 = 7 metres
The grey hound goes 2.75 metres in one leap.
∴ Distance covered by it in 3
leaps
= 3 × 2.75 = 8.25 metres
Distance gained by grey hound in 3 leaps = (8.25 − 7)
= 1.25 metres
Distance covered by hare in 50 leaps = 50 × 1.75 metres
= 87.5 metres
Now, 1.25 metres is gained by grey hound in 3 leaps
∴ 87.5 metres is gained in3 × 87.5 = 210 leaps. 1.25
- In a flight of 600 kms, an aircraft was slowed down due to bad weather. Its average speed for the trip was reduced by 200 km per hr. and the time of flight increased by 30 minutes. Find the duration of flight.
-
View Hint View Answer Discuss in Forum
Let the original speed be x kmph
then, new speed = (x – 200) kmph
According to question,
Time taken with new speed – time taken with original speed= 30 min. i.e 1 hr. 2 ∴ 600 − 600 = 1 x − 200 x 2 ⇒ 600 
1 − 1 
= 1 x − 200 x 2 ⇒ x − x + 200 = 1 x(x − 200) 1200
⇒ 24000 = x (x – 200)
⇒ x2 – 200x – 24000 = 0
⇒ x2 – 600x + 400x – 24000 = 0
⇒ x (x – 600) + 400 (x – 600) = 0
⇒ (x – 600) (x + 400) = 0
⇒ x = 600, – 400
Speed cannot be negative
Hence, original speed = 600 kmph and duration of flight= 600 hr. = 1 hr. 600 Correct Option: B
Let the original speed be x kmph
then, new speed = (x – 200) kmph
According to question,
Time taken with new speed – time taken with original speed= 30 min. i.e 1 hr. 2 ∴ 600 − 600 = 1 x − 200 x 2 ⇒ 600 
1 − 1 
= 1 x − 200 x 2 ⇒ x − x + 200 = 1 x(x − 200) 1200
⇒ 24000 = x (x – 200)
⇒ x2 – 200x – 24000 = 0
⇒ x2 – 600x + 400x – 24000 = 0
⇒ x (x – 600) + 400 (x – 600) = 0
⇒ (x – 600) (x + 400) = 0
⇒ x = 600, – 400
Speed cannot be negative
Hence, original speed = 600 kmph and duration of flight= 600 hr. = 1 hr. 600
- Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels 5 km per hr. faster than the second train. If after two hours they are 50 km apart, find the average speed of faster train.
-
View Hint View Answer Discuss in Forum
Let the speed of the second train be x km per hr. Then the speed of the first train is x + 5 km per hr.
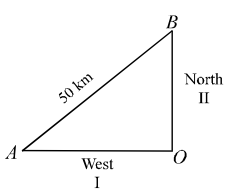
Let O be the position of the railway station from which the two trains leave. Distance travelled by the first train in 2 hours = OA = 2 (x + 5) km.
Distance travelled by the 2nd train in 2 hours= OB = 2x km.
By Pythagoras theorem,
AB2 + OA2 + OB2
⇒ 502 = [2 (x + 5)]2 + [2x]2
⇒ 2500 = 4 (x + 5)2 + 4x2
⇒ 2500 = 4 (x2 + 10x + 25) + 4x2
⇒ 8x2 + 40x – 2400 = 0
⇒ x2 + 5x – 300 = 0
⇒ x2 + 20x – 15x – 300 = 0
⇒ x (x + 20) – 15 (x + 20) = 0
⇒ (x – 15) (x + 20) = 0
⇒ x = 15, – 20
But x cannot be negative
∴ x = 15
∴ The speed of the second train is 15 km per hr. and the speed of the first train is 20 km per hr.Correct Option: C
Let the speed of the second train be x km per hr. Then the speed of the first train is x + 5 km per hr.

Let O be the position of the railway station from which the two trains leave. Distance travelled by the first train in 2 hours = OA = 2 (x + 5) km.
Distance travelled by the 2nd train in 2 hours= OB = 2x km.
By Pythagoras theorem,
AB2 + OA2 + OB2
⇒ 502 = [2 (x + 5)]2 + [2x]2
⇒ 2500 = 4 (x + 5)2 + 4x2
⇒ 2500 = 4 (x2 + 10x + 25) + 4x2
⇒ 8x2 + 40x – 2400 = 0
⇒ x2 + 5x – 300 = 0
⇒ x2 + 20x – 15x – 300 = 0
⇒ x (x + 20) – 15 (x + 20) = 0
⇒ (x – 15) (x + 20) = 0
⇒ x = 15, – 20
But x cannot be negative
∴ x = 15
∴ The speed of the second train is 15 km per hr. and the speed of the first train is 20 km per hr.

