Speed, Time and Distance
-
reaches school 20 minutes earlier. Find his usual time.By walking 5 of usual speed a student 3
-
View Hint View Answer Discuss in Forum
5/3 of usual speed means 3/5 of usual time as he reaches earlier.
∴ 3 usual time + 20 minutes = Usual time 5 20 minutes = 
1 − 3 
usual time 5 = 2 usual time 5 ∴ Usual time = 20 × 5 = 50 minutes. 2 Correct Option: B
5/3 of usual speed means 3/5 of usual time as he reaches earlier.
∴ 3 usual time + 20 minutes = Usual time 5 20 minutes = 
1 − 3 
usual time 5 = 2 usual time 5 ∴ Usual time = 20 × 5 = 50 minutes. 2
- A man covers one-third of his journey at 30 km per hr. and the remaining two-third at 45 km per hr. If the total journey is of 150 kms, what is his average speed for the whole journey?
-
View Hint View Answer Discuss in Forum
Length of journey = 150 kms
1 rd of journey = 150 = 50 kms 3 3 Remaining 2 journey 3
= 150 – 50 = 100 kmsTime taken in 1 rd journey at 30 km per hr. 3 t1 = 50 = 5 hrs. 30 3 Time taken in 2 rd journey at 45 km per hr. 3 t2 = 100 = 20 hrs. 45 9
Total time taken in whole journey = t1 + t2= 5 + 20 = 15 + 20 = 35 hrs. 3 9 9 9 Average Speed = 150 = 150 × 9 = 270 35/9 35 7 = 38 4 km per hr. 7 Correct Option: B
Length of journey = 150 kms
1 rd of journey = 150 = 50 kms 3 3 Remaining 2 journey 3
= 150 – 50 = 100 kmsTime taken in 1 rd journey at 30 km per hr. 3 t1 = 50 = 5 hrs. 30 3 Time taken in 2 rd journey at 45 km per hr. 3 t2 = 100 = 20 hrs. 45 9
Total time taken in whole journey = t1 + t2= 5 + 20 = 15 + 20 = 35 hrs. 3 9 9 9 Average Speed = 150 = 150 × 9 = 270 35/9 35 7 = 38 4 km per hr. 7
- Two men A and B walk from X to Y a distance of 42 kms at 5 km and 7 km an hour respectively. B reaches Y and returns immediately and meets A at R. Find the distance from X to R.
-
View Hint View Answer Discuss in Forum
When B meets A at R, by then B has walked a distance (XY + YR) and A, the distance XR.
That is both of them have together walked twice the distance from X to Y, i.e., 42 kms.
Now, the ratio of speed of A and B is 5 : 7 and they walk 84 kms.
∴ Hence, the distance XR travelled byA = 5 × 84 = 35 kms. 5 + 7 Correct Option: C
When B meets A at R, by then B has walked a distance (XY + YR) and A, the distance XR.
That is both of them have together walked twice the distance from X to Y, i.e., 42 kms.
Now, the ratio of speed of A and B is 5 : 7 and they walk 84 kms.
∴ Hence, the distance XR travelled byA = 5 × 84 = 35 kms. 5 + 7
- Two men A and B start walking simultaneously from P to Q, a distance of 21 kms, at the speed of 3 km and 4 km an hour respectively. B reaches Q, returns immediately and meets A at R. Find the distance from P to R.
-
View Hint View Answer Discuss in Forum
Let A and B meet after time t hours.
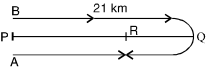
Distance covered by A in t hours = 3 t km.
Distance covered by B in t hours = 4 t km.
Total distance covered by A and B = (3t + 4t) km = 7 t km.
From the diagram we can see that the total distance covered by A and B is equal to twice the distance between P and Q.
∴ 7t = 2 × 21t = 2 × 21 = 6 hours 2
Distance PR = 6 × 3 = 18 km.Correct Option: D
Let A and B meet after time t hours.

Distance covered by A in t hours = 3 t km.
Distance covered by B in t hours = 4 t km.
Total distance covered by A and B = (3t + 4t) km = 7 t km.
From the diagram we can see that the total distance covered by A and B is equal to twice the distance between P and Q.
∴ 7t = 2 × 21t = 2 × 21 = 6 hours 2
Distance PR = 6 × 3 = 18 km.
- Ram travelled one-third of a journey with a speed of 10 km per hr, the next one-third with a speed of 9 km per hr. and the rest at a speed of 8 km per hr. If he had travelled half the journey at speed of 10 km per hr. and the other half with a speed of 8 km per hr, he would have been 1 minute longer on the way. What distance did he travel?
-
View Hint View Answer Discuss in Forum
Let the total distance travelled be x kms.
Case I :
Speed for the first one-third distancei.e. x kms =10 km per hr. 3 ∴ Time taken = x hours 30
Similarly, time taken for the next one-third distance= x hours 27
and time taken for the last onethird distance= x hours. 24
∴ Total time taken to cover x kms.= 
x + x + x 
hours. 30 27 24
Case II :
Time taken for one-half distance at the speed of 10 km per hr.= x hrs. 20
and time taken for remaining 1/2 of distance= x hrs. at 8 km per hr. 16 Total time taken = 
x + x 
hrs. 20 16
Time taken in (Case II – Case I)= 1 minute = 1 hr. 60
∴ According to the questionx + x − 
x + x + x 
20 16 30 27 24 = 1 60 ⇒ 108x + 135x − 72x − 80x − 90x 2160 = 1 60 ⇒ 243x − 242x = 1 2160 60 ⇒ x = 1 2160 60 ⇒ x = 2160 = 36 km. 60
Hence the required distance
= 36 km.Correct Option: A
Let the total distance travelled be x kms.
Case I :
Speed for the first one-third distancei.e. x kms =10 km per hr. 3 ∴ Time taken = x hours 30
Similarly, time taken for the next one-third distance= x hours 27
and time taken for the last onethird distance= x hours. 24
∴ Total time taken to cover x kms.= 
x + x + x 
hours. 30 27 24
Case II :
Time taken for one-half distance at the speed of 10 km per hr.= x hrs. 20
and time taken for remaining 1/2 of distance= x hrs. at 8 km per hr. 16 Total time taken = 
x + x 
hrs. 20 16
Time taken in (Case II – Case I)= 1 minute = 1 hr. 60
∴ According to the questionx + x − 
x + x + x 
20 16 30 27 24 = 1 60 ⇒ 108x + 135x − 72x − 80x − 90x 2160 = 1 60 ⇒ 243x − 242x = 1 2160 60 ⇒ x = 1 2160 60 ⇒ x = 2160 = 36 km. 60
Hence the required distance
= 36 km.

