Speed, Time and Distance
- A train moving at a rate of 36 km/hr. crosses a standing man in 10 seconds. It will cross a platform 55 metres long, in :
-
View Hint View Answer Discuss in Forum
Speed of train = 36 kmph
= 36 × 5 = 10 m/sec 18
Length of train = 10 × 10 = 100 metres∴ Required time = 100 + 55 10 = 15 5 = 15 1 second 10 2
= 15.5 secondsCorrect Option: C
Speed of train = 36 kmph
= 36 × 5 = 10 m/sec 18
Length of train = 10 × 10 = 100 metres∴ Required time = 100 + 55 10 = 15 5 = 15 1 second 10 2
= 15.5 seconds
- A train passes by a lamp post on a platform in 7 sec. and passes by the platform completely in 28 sec. If the length of the platform is 390 m, then length of the train (in metres) is
-
View Hint View Answer Discuss in Forum
Let the length of train be x metre, then
∴ Speed of train = x = x + 390 7 28 ⇒ x = x + 390 4
⇒ 4x – x = 390⇒ x = 390 = 130 metres 3 Correct Option: B
Let the length of train be x metre, then
∴ Speed of train = x = x + 390 7 28 ⇒ x = x + 390 4
⇒ 4x – x = 390⇒ x = 390 = 130 metres 3
- Two trains 100 metres and 95 metres long respectively pass each other in 27 seconds when they run in the same direction and in 9 seconds when they run in opposite directions. Speed of the two trains are
-
View Hint View Answer Discuss in Forum
Let the speed of trains be x and y metre/sec respectively,
100 + 95 = 27 x − y ⇒ x − y = 195 = 65 .....(i) 27 9
Again,195 = 9 x + y ⇒ x + y = 195 .....(ii) 9
By equation (i) + (ii)⇒ 2x = 65 + 195 = 260 9 9 9 ⇒ x = 260 = 130 m/sec. 2 × 9 9 = 
130 × 18 
kmph = 52 kmph 9 5
From equation (ii),y = 195 − 130 = 65 m/sec. 9 9 9 = 65 × 18 = 26 kmph 9 5 Correct Option: B
Let the speed of trains be x and y metre/sec respectively,
100 + 95 = 27 x − y ⇒ x − y = 195 = 65 .....(i) 27 9
Again,195 = 9 x + y ⇒ x + y = 195 .....(ii) 9
By equation (i) + (ii)⇒ 2x = 65 + 195 = 260 9 9 9 ⇒ x = 260 = 130 m/sec. 2 × 9 9 = 
130 × 18 
kmph = 52 kmph 9 5
From equation (ii),y = 195 − 130 = 65 m/sec. 9 9 9 = 65 × 18 = 26 kmph 9 5
- Points ‘A’ and ‘B’ are 70 km apart on a highway. A car starts from ‘A’ and another from ‘B’ at the same time. If they travel in the same direction, they meet in 7 hours, but if they travel towards each-other, they meet in one hour. Find the speed of the two cars (in km/hr).
-
View Hint View Answer Discuss in Forum
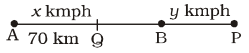
Let speed of car starting from A be x kmph
and speed of car starting from B be y kmph
Case I
When cars meet at P,
7x = AP = AB + BP = 70 + 7y
⇒ 7x – 7y = 70
⇒ x – y = 10 ...(i)
Case II
When cars meet at Q,
x + y = 70 ...(ii)
On adding these equations,
x = 40 kmph
Putting the value of x in equation (i),
y = 40 – 10 = 30 kmphCorrect Option: B

Let speed of car starting from A be x kmph
and speed of car starting from B be y kmph
Case I
When cars meet at P,
7x = AP = AB + BP = 70 + 7y
⇒ 7x – 7y = 70
⇒ x – y = 10 ...(i)
Case II
When cars meet at Q,
x + y = 70 ...(ii)
On adding these equations,
x = 40 kmph
Putting the value of x in equation (i),
y = 40 – 10 = 30 kmph
- A train crosses a pole in 15 seconds and a platform 100 metres long in 25 seconds. Its length (in metres) is
-
View Hint View Answer Discuss in Forum
Let the length of train be x metre.
∴ x = x + 100 15 25 ⇒ x = x + 100 3 5
⇒ 5x = 3x + 300
⇒ 2x = 300⇒ x = 300 = 150 metres 2 Correct Option: C
Let the length of train be x metre.
∴ x = x + 100 15 25 ⇒ x = x + 100 3 5
⇒ 5x = 3x + 300
⇒ 2x = 300⇒ x = 300 = 150 metres 2

