Trigonometry
- What is the angle in radian through which a pendulum swings and its length is 75 cm and the tip describes an arc of length 21 cm.
-
View Hint View Answer Discuss in Forum
We know that,
Angle = arc radius ⇒ θ = 21 75 θ = 
7 
R 25 
Correct Option: B
We know that,
Angle = arc radius ⇒ θ = 21 75 θ = 
7 
R 25 
- What will be the radius of circle in which a central angle of 60° intercepts an arc of length 37.4 cm.
-
View Hint View Answer Discuss in Forum
Here,
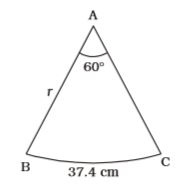
θ = 60°
l = 37.4 cm
r = ?
We know that,1° = 
π 
R 180° ⇒ 60° = 
π × 60 
R 180° ⇒ 60° = 
π 
R 3
We know that,θ = l r ⇒ π = 37.4 3 4 ⇒ r = 37.4 × 3 π r = 37.4 × 3 × 7 22
= 1.7 × 21 = 35.7 cmCorrect Option: C
Here,

θ = 60°
l = 37.4 cm
r = ?
We know that,1° = 
π 
R 180° ⇒ 60° = 
π × 60 
R 180° ⇒ 60° = 
π 
R 3
We know that,θ = l r ⇒ π = 37.4 3 4 ⇒ r = 37.4 × 3 π r = 37.4 × 3 × 7 22
= 1.7 × 21 = 35.7 cm
- What is the value of cosec (–1410°) ?
-
View Hint View Answer Discuss in Forum
cosec (–1410°) = – cosec (1410°)
∵cosec (– θ)
= – cosecθ = –cosec (360° × 3 + 330°)
= –cosec (330°) = –cosec (360° – 30°)
= cosec 30°
= 2Correct Option: B
cosec (–1410°) = – cosec (1410°)
∵cosec (– θ)
= – cosecθ = –cosec (360° × 3 + 330°)
= –cosec (330°) = –cosec (360° – 30°)
= cosec 30°
= 2
-
The value of cos 
π + x 
+ cos 
π - x 
will be 4 4
-
View Hint View Answer Discuss in Forum
cos 
π + x 
+ cos 
π - x 
4 4 = 2cos 
π + x - π - x 
cos 
π + x - π + x 
4 4 4 4 2 2
∵ cosC + cosD= 2cos 
C + D 
cos 
C - D 
2 2 = 2cos 
π 
cosx 4 = 2 .cosx √2
= √2cosxCorrect Option: B
cos 
π + x 
+ cos 
π - x 
4 4 = 2cos 
π + x - π - x 
cos 
π + x - π + x 
4 4 4 4 2 2
∵ cosC + cosD= 2cos 
C + D 
cos 
C - D 
2 2 = 2cos 
π 
cosx 4 = 2 .cosx √2
= √2cosx
- If cosq = – 1/2 and θ lies in third quadrant, then what will be the value of sinθ + tanθ
-
View Hint View Answer Discuss in Forum
Here, cosθ = – 1/2 and θ, lies in third quadrant
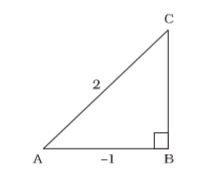
Consider ∆ABC,
Using Pythagoras theorem,
AC² = AB² + BC²
2² = (–1)² + BC²
⇒ BC² = 4 – 1
BC² = 3
BC = √3tanθ + sinθ = – 
√3 
+ - 
√3 
- 1 2
∵ In third quadrant sinθ is negative and tanθ is positive.
== √3 2 Correct Option: C
Here, cosθ = – 1/2 and θ, lies in third quadrant

Consider ∆ABC,
Using Pythagoras theorem,
AC² = AB² + BC²
2² = (–1)² + BC²
⇒ BC² = 4 – 1
BC² = 3
BC = √3tanθ + sinθ = – 
√3 
+ - 
√3 
- 1 2
∵ In third quadrant sinθ is negative and tanθ is positive.
== √3 2

