Trigonometry
- The angle of elevation of an aeroplane from a point A on the ground is 60°. After a straight flight of the plane for 30 seconds, the angle of elevation becomes 30°. If the palne flies at a constant height of 3600√3 metre, what is the speed of plane?
-
View Hint View Answer Discuss in Forum
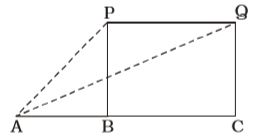
P and Q = Positions of plane
∠PAB = 60°, ∠QAB = 30°, PB = 3600√3 metre
In ∆ABP,tan 60° = BP AB ⇒ √3 = 3600√3 AB
⇒ AB = 3600 metre
In ∆ACQ,tan 30° = CQ AC ⇒ 1 = 3600√3 √3 AC
⇒ AC = 3600 × 3 = 10800 metre
∴ PQ = BC = AC – AB = 10800 – 3600 = 7200 metre
This distance is covered in 30 seconds.∴ Speed of plane = 7200 = 240 m/sec. 30
= 240= 
240 × 18 
5
= 864 kmphCorrect Option: A

P and Q = Positions of plane
∠PAB = 60°, ∠QAB = 30°, PB = 3600√3 metre
In ∆ABP,tan 60° = BP AB ⇒ √3 = 3600√3 AB
⇒ AB = 3600 metre
In ∆ACQ,tan 30° = CQ AC ⇒ 1 = 3600√3 √3 AC
⇒ AC = 3600 × 3 = 10800 metre
∴ PQ = BC = AC – AB = 10800 – 3600 = 7200 metre
This distance is covered in 30 seconds.∴ Speed of plane = 7200 = 240 m/sec. 30
= 240= 
240 × 18 
5
= 864 kmph
- sin 75° + sin 15° can be expressed as
-
View Hint View Answer Discuss in Forum
sin 75° + sin 15° = 2 sin
= 
75° + 15° 
. cos 
75° - 15° 
2 2
∵ sinC + sinD= 2sin 
C + D 
. cos 
C - D 
2 2
= 2 sin 45° . cos 30°= 2 . 1 . √3 √2 2
√3/2Correct Option: D
sin 75° + sin 15° = 2 sin
= 
75° + 15° 
. cos 
75° - 15° 
2 2
∵ sinC + sinD= 2sin 
C + D 
. cos 
C - D 
2 2
= 2 sin 45° . cos 30°= 2 . 1 . √3 √2 2
√3/2
- What will be the value of 2 cos 45° × sin 15°
-
View Hint View Answer Discuss in Forum
We know that,
2 cosA sinB = sin(A + B) – sin(A – B)
⇒ 2 cos 45° sin 15°
= sin (45° + 15°) – sin (45° – 15°)
= sin 60° – sin 30°= √3 - 1 2 2 = √3 - 1 1 Correct Option: C
We know that,
2 cosA sinB = sin(A + B) – sin(A – B)
⇒ 2 cos 45° sin 15°
= sin (45° + 15°) – sin (45° – 15°)
= sin 60° – sin 30°= √3 - 1 2 2 = √3 - 1 1
-
The value of sin 22 1° will be 2
-
View Hint View Answer Discuss in Forum
We know that,
cos2A = 1 – 2 sin²A⇒ cosA = 1 – 2 sin² A 2
Let A = 45°⇒ cos 45° = 1 – 2 sin² 45° 2 ⇒ 2 sin² 22 1° = 1 – cos 45° 2 ⇒ 2 sin² 22 1° = 1 – 1 2 √2 ⇒ 2 sin² 22 1° = √2 - 1 2 √2 ⇒ 2 sin² 22 1° = √2 - 1 2 2√2 ⇒ 2 sin² 22 1° = √ √2 - 1 2 2√2 Correct Option: D
We know that,
cos2A = 1 – 2 sin²A⇒ cosA = 1 – 2 sin² A 2
Let A = 45°⇒ cos 45° = 1 – 2 sin² 45° 2 ⇒ 2 sin² 22 1° = 1 – cos 45° 2 ⇒ 2 sin² 22 1° = 1 – 1 2 √2 ⇒ 2 sin² 22 1° = √2 - 1 2 √2 ⇒ 2 sin² 22 1° = √2 - 1 2 2√2 ⇒ 2 sin² 22 1° = √ √2 - 1 2 2√2
-
The value of cosα + cosβ will be sinα + sinβ
-
View Hint View Answer Discuss in Forum
cosα + cosβ sinα + sinβ = 2.cos 
α + β 
cos 
α - β 
2 2 2.sin 
α + β 
sin 
α - β 
2 2 = cos 
α + β 
2 sin 
α + β 
2 = cot 
α + β 
2 Correct Option: B
cosα + cosβ sinα + sinβ = 2.cos 
α + β 
cos 
α - β 
2 2 2.sin 
α + β 
sin 
α - β 
2 2 = cos 
α + β 
2 sin 
α + β 
2 = cot 
α + β 
2

