Trigonometry
- If cosx . cosy + sinx . siny = –1 then cosx + cosy is
-
View Hint View Answer Discuss in Forum
cosx . cosy + sinx. siny = –1
⇒ cosx . cosy + 1 = – sinx . siny On squaring both sides, (cosx . cosy + 1)² = sin²x sin²y
⇒ cos²x . cos²y + 2cosx . cosy + 1 = (1 – cos²x) (1 – cos²y)
⇒ cos²x . cos2y + 2 cosx. cosy + 1 = 1 – cos²x – cos²y + cos²x . cos²y
⇒ cos²x + cos2y + 2cosx . cosy = 0
⇒ (cosx + cosy)² = 0
⇒ cosx + cosy = 0Correct Option: C
cosx . cosy + sinx. siny = –1
⇒ cosx . cosy + 1 = – sinx . siny On squaring both sides, (cosx . cosy + 1)² = sin²x sin²y
⇒ cos²x . cos²y + 2cosx . cosy + 1 = (1 – cos²x) (1 – cos²y)
⇒ cos²x . cos2y + 2 cosx. cosy + 1 = 1 – cos²x – cos²y + cos²x . cos²y
⇒ cos²x + cos2y + 2cosx . cosy = 0
⇒ (cosx + cosy)² = 0
⇒ cosx + cosy = 0
- ABC is a right angled triangle with ∠A = 90°. Then the value of cos²A + cos²B + cos²C is :
-
View Hint View Answer Discuss in Forum
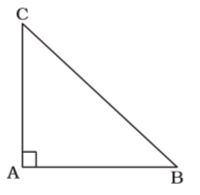
∠CAB = 90°
∴ cosA = cos 90° = 0cosB = AB , cosC = AC BC BC
∴ cos²A + cos²B + cos²C= 0 + AB² + AC² BC² BC² = AB² + AC² = BC² = 1 BC² BC² Correct Option: B

∠CAB = 90°
∴ cosA = cos 90° = 0cosB = AB , cosC = AC BC BC
∴ cos²A + cos²B + cos²C= 0 + AB² + AC² BC² BC² = AB² + AC² = BC² = 1 BC² BC²
- If r sinθ = 7/2 and r cosθ = 7√3/2 then the value of θ is :
-
View Hint View Answer Discuss in Forum
r sinθ = 7 2 r cosθ = 7√3 2 ⇒ rsinθ = 7/2 rcosθ 7√3/2 ⇒ tanθ = 7 × 2 = 1 2 7√3 √3
⇒ tanθ = tan30°
⇒ θ = 30°Correct Option: A
r sinθ = 7 2 r cosθ = 7√3 2 ⇒ rsinθ = 7/2 rcosθ 7√3/2 ⇒ tanθ = 7 × 2 = 1 2 7√3 √3
⇒ tanθ = tan30°
⇒ θ = 30°
-
If tanq = 1, then the value of 8sinθ + 5cosθ is : sin²θ - 2cos²θ + 7cosθ
-
View Hint View Answer Discuss in Forum
Expression = 8sinθ + 5cosθ sin³θ - 2cos³θ + 7cosθ
Dividing numerator and denominator by cos³θ= 8sinθ + 5cosθ cos³θ cos³θ sin³θ - 2cos³θ + 7cosθ cos³θ cos³θ cos³θ = 8tanθ.sec²θ + 5cos²θ tan³θ - 2 + 7(1 + tan²θ) = 16 + 10 × 2 1 - 2 + 7(1 + 1) = 8(1 + 1) + 1 - 2 + 14 = 26 = 2 13 Correct Option: C
Expression = 8sinθ + 5cosθ sin³θ - 2cos³θ + 7cosθ
Dividing numerator and denominator by cos³θ= 8sinθ + 5cosθ cos³θ cos³θ sin³θ - 2cos³θ + 7cosθ cos³θ cos³θ cos³θ = 8tanθ.sec²θ + 5cos²θ tan³θ - 2 + 7(1 + tan²θ) = 16 + 10 × 2 1 - 2 + 7(1 + 1) = 8(1 + 1) + 1 - 2 + 14 = 26 = 2 13
- If θ is positive acute angle and 4 sin²θ = 3, then the value of

tanθ - cot θ 
is : 2
-
View Hint View Answer Discuss in Forum
4 sin²θ = 3
⇒ sin²θ = 3/4⇒ sinθ = √3 = sin 60° 2
⇒ θ = 60°&threre4; tanθ – cot θ 2
= tan 60° – cot 30° = √3 – √3 = 0Correct Option: B
4 sin²θ = 3
⇒ sin²θ = 3/4⇒ sinθ = √3 = sin 60° 2
⇒ θ = 60°&threre4; tanθ – cot θ 2
= tan 60° – cot 30° = √3 – √3 = 0

