Trigonometry
-
If cosx = – 3 and p < x < 3π , then the value of sin 2x will be 5 2
-
View Hint View Answer Discuss in Forum
Here,
cosx = – 3 and p < x < 3π 5 2
⇒ x lies in third quadrant, and we know that in third quadrant only tan and cot are positive.
Consider right angled ∆ABC,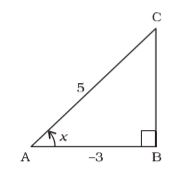
Using pythagoras theorem,
AC² = AB² + BC²
⇒ 5² = (–3)² + BC²
16 = BC²
⇒ BC = 4
We know that,
sin2A = 2sinA × cosA
⇒ sin2x = 2 × sinx× cosx= 2 × 
- 4 
× - 3 5 5 = 24 25
∵ Here, sinq is –veCorrect Option: C
Here,
cosx = – 3 and p < x < 3π 5 2
⇒ x lies in third quadrant, and we know that in third quadrant only tan and cot are positive.
Consider right angled ∆ABC,
Using pythagoras theorem,
AC² = AB² + BC²
⇒ 5² = (–3)² + BC²
16 = BC²
⇒ BC = 4
We know that,
sin2A = 2sinA × cosA
⇒ sin2x = 2 × sinx× cosx= 2 × 
- 4 
× - 3 5 5 = 24 25
∵ Here, sinq is –ve
- What is the value of tan 330° ?
-
View Hint View Answer Discuss in Forum
tan 330° = tan(360° – 30°)
= –tan 30°
∵ tan(360° - θ) - tanθ= - 1 √2 Correct Option: D
tan 330° = tan(360° – 30°)
= –tan 30°
∵ tan(360° - θ) - tanθ= - 1 √2
-
The degree measure of 
5π 
will be 12
-
View Hint View Answer Discuss in Forum
We know that,
1R = 
180° 
= 5π R = 
180° × 5π 
° = 75° π 12 π 12 Correct Option: B
We know that,
1R = 
180° 
= 5π R = 
180° × 5π 
° = 75° π 12 π 12
- If sin (2a + 45°) = cos (30° – a), where 0° < a < 90°, then the value of a is :
-
View Hint View Answer Discuss in Forum
sin (2a + 45°) = cos (30° – a)
⇒ sin (2a + 45°) = sin {90° – (30° – a) }
⇒ sin (2a + 45°) = sin (60° + a)
[∵ sin (90° – θ) = cosθ]
⇒ 2a + 45° = 60° + a
⇒ 2a – a = 60° - 45°
⇒ a = 15°Correct Option: B
sin (2a + 45°) = cos (30° – a)
⇒ sin (2a + 45°) = sin {90° – (30° – a) }
⇒ sin (2a + 45°) = sin (60° + a)
[∵ sin (90° – θ) = cosθ]
⇒ 2a + 45° = 60° + a
⇒ 2a – a = 60° - 45°
⇒ a = 15°
- The least value of tan²x + cot²x is:
-
View Hint View Answer Discuss in Forum
The minimum value of a tan²x + b cot²x = 2√ab
∴ The minimum value of tan²x + cot²x = 2Correct Option: B
The minimum value of a tan²x + b cot²x = 2√ab
∴ The minimum value of tan²x + cot²x = 2

