Algebra
- The linear equation such that each point on its graph has an ordinate four times its abscissa is :
-
View Hint View Answer Discuss in Forum
Check through options y = 4x,
When, x = 1, y = 4Correct Option: B
Check through options y = 4x,
When, x = 1, y = 4
- If the graph of the equations 3x + 2y = 18 and 3y – 2x = 1 intersect at the point (p, q), then the value of p + q is
-
View Hint View Answer Discuss in Forum
3x + 2y = 18 ...(i)
3y – 2x = 1 ...(ii)
By equation (i) × 2 + (ii) × 3 gives,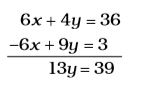
⇒ y = 3 Putting y = 3 in (ii)
3(3) – 2x = 1 ⇒ x = 4
∴ (p, q) = (4, 3) and hence, p + q = 7Correct Option: A
3x + 2y = 18 ...(i)
3y – 2x = 1 ...(ii)
By equation (i) × 2 + (ii) × 3 gives,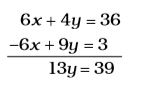
⇒ y = 3 Putting y = 3 in (ii)
3(3) – 2x = 1 ⇒ x = 4
∴ (p, q) = (4, 3) and hence, p + q = 7
- If the graph of the equations x + y = 0 and 5y + 7x = 24 intersect at (m, n), then the value of m + n is
-
View Hint View Answer Discuss in Forum
On putting y = –x in the equation 5y + 7x = 24,
–5x + 7x = 24
⇒ 2x = 24 ⇒ x = 12 & y = –12
∴ m = x = 12, n = y = –12
⇒ m + n = 12 – 12 = 0Correct Option: C
On putting y = –x in the equation 5y + 7x = 24,
–5x + 7x = 24
⇒ 2x = 24 ⇒ x = 12 & y = –12
∴ m = x = 12, n = y = –12
⇒ m + n = 12 – 12 = 0
- The area of the triangle formed by the graph of 3x + 4y = 12, x axis and y-axis (in sq. units) is
-
View Hint View Answer Discuss in Forum

x – axis Þ y = 0, putting in equation 3x + 4y = 12 3x = 12 ⇒ x = 4
⇒ Co-ordinates of point of intersection on x-axis = (4, 0)
Putting x = 0 in the equation 3x + 4y = 12 4y = 12 ⇒ y = 3
∴ Co-ordinates of point of intersection on y – axis = (0, 3)
∴ OA = 4
OB = 3∴ Area of ∴OAB = 1 × OA × OB 1 × 4 × 3 = 6 sq. units 2 2 Correct Option: C

x – axis Þ y = 0, putting in equation 3x + 4y = 12 3x = 12 ⇒ x = 4
⇒ Co-ordinates of point of intersection on x-axis = (4, 0)
Putting x = 0 in the equation 3x + 4y = 12 4y = 12 ⇒ y = 3
∴ Co-ordinates of point of intersection on y – axis = (0, 3)
∴ OA = 4
OB = 3∴ Area of ∴OAB = 1 × OA × OB 1 × 4 × 3 = 6 sq. units 2 2
- If 4x + 5y = 83 and 3x : 2y = 21 : 22, then (y – x) equals
-
View Hint View Answer Discuss in Forum
3x = 21 2y 22 ⇒ x = 21 × 2 = 7 y 22 3 11 ⇒ x = y = k 7 11
∴ 4x + 5y = 83
⇒ 4 × 7k + 5 × 11k = 83
⇒ 28k + 55k = 83
⇒ 83k = 83
⇒ k = 1
∴ x = 7, y = 11
∴ y – x = 11 – 7 = 4Correct Option: B
3x = 21 2y 22 ⇒ x = 21 × 2 = 7 y 22 3 11 ⇒ x = y = k 7 11
∴ 4x + 5y = 83
⇒ 4 × 7k + 5 × 11k = 83
⇒ 28k + 55k = 83
⇒ 83k = 83
⇒ k = 1
∴ x = 7, y = 11
∴ y – x = 11 – 7 = 4

