91. What is the equation of a line perpendicular to the line x – 7y + 5 = 0 and having x-intercept 3?

1. 1. x + 7y = 21

   
   
   

   2. 7x + y = 21

   
   
   

   3. x + 2y = 10

   
   
   

   4. –x + y = 15

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let the slope of line be m Here,
   

   m1 =	- 1	=	1
   	- 7		7

   
   As lines are perpendicular,
   ∴ m₁ × m₂ = –1
   

   m ×	1	= - 1
   	7

   
   m = –7
   ∴ Equation of line is (y – y₁) = m(x – x₁) (y – 0)
   = –7(x – 3) y = –7x + 21
   ⇒ 7x + y = 21

   Correct Option: B

   Let the slope of line be m Here,
   

   m1 =	- 1	=	1
   	- 7		7

   
   As lines are perpendicular,
   ∴ m₁ × m₂ = –1
   

   m ×	1	= - 1
   	7

   
   m = –7
   ∴ Equation of line is (y – y₁) = m(x – x₁) (y – 0)
   = –7(x – 3) y = –7x + 21
   ⇒ 7x + y = 21

---

92. For what value of k the line (k – 3)x – (4 – k²)y + k² – 7k + 6 = 0 is parallel to x-axis ?

1. 1. k = ± 1

   
   
   

   2. k = ± 4

   
   
   

   3. k = ± 6

   
   
   

   4. k = ± 2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   We know that when a line is parallel to x-axis then Slope = 0
   

   	(4 - k²)	= 0
   	k - 3

   
   4 – k² = 0
   k² = 4
   k = √4
   k = ± 2

   Correct Option: D

   We know that when a line is parallel to x-axis then Slope = 0
   

   	(4 - k²)	= 0
   	k - 3

   
   4 – k² = 0
   k² = 4
   k = √4
   k = ± 2

---

---

93. In what ratio, the line joining (– 1, 1) and (5, 7) is divided by the line x + y = 4 ?

1. 1. 5 : 13

   
   
   

   2. 5 : 2

   
   
   

   3. 1 : 3

   
   
   

   4. 4 : 7

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let the ratio be k : 1
   
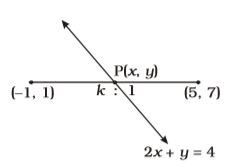
   Using internal section formula,
   

   x =	5k - 1	= 0
   	k + 1

   
   

   y =	7k + 1	= 0
   	k + 1

   
   Putting the value of x and y in given equation 2x + y = 4
   

   2		5k - 1		+	7k + 1	= 4
   		k + 1			k + 1

   
   10k – 2 + 7k + 1 = 4 (k + 1)
   17k – 1 = 4k + 4
   13k = 5
   

   k =	5	= 0
   	13

   
   ∴ The ratio is 5 : 13

   Correct Option: A

   Let the ratio be k : 1
   
   Using internal section formula,
   

   x =	5k - 1	= 0
   	k + 1

   
   

   y =	7k + 1	= 0
   	k + 1

   
   Putting the value of x and y in given equation 2x + y = 4
   

   2		5k - 1		+	7k + 1	= 4
   		k + 1			k + 1

   
   10k – 2 + 7k + 1 = 4 (k + 1)
   17k – 1 = 4k + 4
   13k = 5
   

   k =	5	= 0
   	13

   
   ∴ The ratio is 5 : 13

---

94. The distance between the lines y = mx + c₁ and y = mx + c₁ is

1. 1. c1 - c2

      √m² + 1

   
   
   

   2. 	c1 - c2
      	√1 + m²

   
   
   

   3. c2 - c1

      √1 + m²

   
   
   

   4. 0

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let the distance between the lines be d
   
   Also we know that
   y – mx = c₂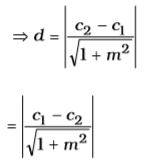
   

   Correct Option: B

   Let the distance between the lines be d
   
   Also we know that
   y – mx = c₂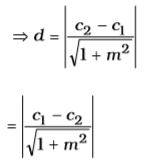
   

---

---

95. A point equidistant from the lines 4x + 3y + 10 = 0, 5x – 12y + 26 = 0 and 7x + 24y – 50 = 0 is

1. 1. (1, –1)

   
   
   

   2. (1, 1)

   
   
   

   3. (0, 0)

   
   
   

   4. (0, 1)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Here, it is clear that distance of the given lines from (0, 0) is equal.
   

   d1 =		y - mx - c1
   		√1 + m²

   
   

   =		10
   		5

   
   = 2 units
   

   d2 =		5 × 0 - 12 × 0 + 26
   		√5² + 12²

   
   

   =		26
   		13

   
   = 2 units
   

   d3 =		7 × 0 + 24 × 0 - 50
   		√7² + 24²

   
   

   =		- 50
   		√625

   
   

   =		50
   		√25

   
   d₃ = 2

   Correct Option: C

   Here, it is clear that distance of the given lines from (0, 0) is equal.
   

   d1 =		y - mx - c1
   		√1 + m²

   
   

   =		10
   		5

   
   = 2 units
   

   d2 =		5 × 0 - 12 × 0 + 26
   		√5² + 12²

   
   

   =		26
   		13

   
   = 2 units
   

   d3 =		7 × 0 + 24 × 0 - 50
   		√7² + 24²

   
   

   =		- 50
   		√625

   
   

   =		50
   		√25

   
   d₃ = 2

---