81. Find the co-ordinates of the mid point of a line segment joining the points (2, 4) and (6, 8) ?

1. 1. (2, 6)

   
   
   

   2. (4, 6)

   
   
   

   3. (6, 4)

   
   
   

   4. (–4, –6)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   We know that co-ordinates of
   

   	x1 + x2	,	y1 + y2
   	2		2

   
   

   ⇒ x =	2 + 6	= 4
   	2

   
   

   y =	4 + 8	= 6
   	2

   Correct Option: B

   We know that co-ordinates of
   

   	x1 + x2	,	y1 + y2
   	2		2

   
   

   ⇒ x =	2 + 6	= 4
   	2

   
   

   y =	4 + 8	= 6
   	2

---

82. For what value of k, the line kx + 3y + 6 = 0, will pass through the point (2, 4).

1. 1. k = –8

   
   
   

   2. k = 7

   
   
   

   3. k = –9

   
   
   

   4. k = 6

   
   
   

---

1. View Hint View Answer Discuss in Forum

   As the line kx + 3y + 6 = 0
   passes through (2, 4)
   ∴ k × 2 + 3 × 4 + 6 = 0
   2k + 12 + 6 = 0
   2k + 18 = 0
   2k = –18 k = –9

   Correct Option: C

   As the line kx + 3y + 6 = 0
   passes through (2, 4)
   ∴ k × 2 + 3 × 4 + 6 = 0
   2k + 12 + 6 = 0
   2k + 18 = 0
   2k = –18 k = –9

---

---

83. In what ratio the line segment joining the points (2, 3) and (4, 6) is divided by y-axis?

1. 1. Internally 1 : 2

   
   
   

   2. Externally 2 : 3

   
   
   

   3. Externally 2 : 1

   
   
   

   4. Externally 1 : 2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let the co-ordinates of point be (0, y) because on y-axis, x is zero.
   Let the ratio be k : 1
   Using internal section formula, we get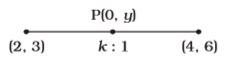
   
   

   0 =	4k + 2
   	k + 1

   
   

   k =	- 2
   	4

   
   

   k =	- 1
   	2

   
   –ve sign shows that point divides the line segment externally.

   Correct Option: D

   Let the co-ordinates of point be (0, y) because on y-axis, x is zero.
   Let the ratio be k : 1
   Using internal section formula, we get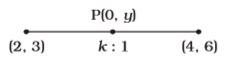
   
   

   0 =	4k + 2
   	k + 1

   
   

   k =	- 2
   	4

   
   

   k =	- 1
   	2

   
   –ve sign shows that point divides the line segment externally.

---

84. What is the equation of line passes through the point (3, 2) and make an angle of 45° with the line x – 2y = 3 ?

1. 1. 3 x – y – 7 = 0

   
   
   

   2. 3 x + y = 7

   
   
   

   3. x – 3y = 7

   
   
   

   4. –3x + y = 6

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let the slope of line be m
   Here,
   θ = 45°
   

   m2 =	- 1	=	1
   	- 2		2

   
   We know that,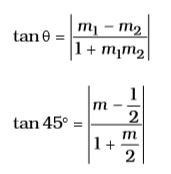
   
   

   1 =	2m - 1
   	2 + 3

   
   ⇒ 2 + m = 2m – 1
   m = 3
   ∴ Equation of line be
   y – y₁ = m(x – x₁)
   y – 2 = 3(x – 3)
   y – 2 = 3x – 9
   3x – y – 7 = 0

   Correct Option: A

   Let the slope of line be m
   Here,
   θ = 45°
   

   m2 =	- 1	=	1
   	- 2		2

   
   We know that,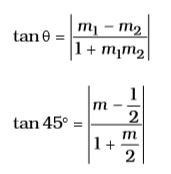
   
   

   1 =	2m - 1
   	2 + 3

   
   ⇒ 2 + m = 2m – 1
   m = 3
   ∴ Equation of line be
   y – y₁ = m(x – x₁)
   y – 2 = 3(x – 3)
   y – 2 = 3x – 9
   3x – y – 7 = 0

---

---

85. A point R(h, k) divides a line segment between the axis in the ratio 1 : 2 what will be the equation of line ?

1. 1. x	-	2y	= 4
      h		k

   
   
   

   2. x	+	2y	= 3
      h		k

   
   
   

   3. x	+	y	= 1
      k		h

   
   
   

   4. x	+	y	= 1
      2k		h

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using internal section formula, we have
   
   

   h =	1 × a + 2 × 0
   	1 + 2

   
   ⇒a = 3h
   Similarly,
   

   k =	1 × 0 + 2 × b
   	1 + 2

   
   

   k =	2b
   	3

   
   

   b =	3k
   	2

   
   ∴ Equation of line be
   

   	x	+	y	= 1
   	a		b

   
   

   ⇒	x	+	2y	= 1
   	3h		3k

   
   

   ⇒	x	+	2y	= 3
   	h		k

   Correct Option: B

   Using internal section formula, we have
   
   

   h =	1 × a + 2 × 0
   	1 + 2

   
   ⇒a = 3h
   Similarly,
   

   k =	1 × 0 + 2 × b
   	1 + 2

   
   

   k =	2b
   	3

   
   

   b =	3k
   	2

   
   ∴ Equation of line be
   

   	x	+	y	= 1
   	a		b

   
   

   ⇒	x	+	2y	= 1
   	3h		3k

   
   

   ⇒	x	+	2y	= 3
   	h		k

---