Algebra
- What will be the equation of line for which p = 3 and a = 120° ?
-
View Hint View Answer Discuss in Forum
Here,
p = 3 and α = 120°
We know that equation of line is x cosα + y sinα = p
⇒ x cos 120° + y sin 120° = 3
⇒ x cos (180° – 60°) + y sin (180° – 60°) = 3
⇒ – x cos 60° + y sin 60° = 3
∵ cos (180° – θ) = –cosθ
sin (180° – θ) = sinθ⇒ - x + y √3 = 3 2 2
⇒ – x + √3y = 6Correct Option: C
Here,
p = 3 and α = 120°
We know that equation of line is x cosα + y sinα = p
⇒ x cos 120° + y sin 120° = 3
⇒ x cos (180° – 60°) + y sin (180° – 60°) = 3
⇒ – x cos 60° + y sin 60° = 3
∵ cos (180° – θ) = –cosθ
sin (180° – θ) = sinθ⇒ - x + y √3 = 3 2 2
⇒ – x + √3y = 6
- If the points (h, o), (a, b) and (o, k) lie on a line, then?
-
View Hint View Answer Discuss in Forum
We know that when three points are collinear than area of triangle is zero.
ar∆ = 
h 0 1 
1 a b 1 2 a b 1 ⇒ 1 [h(b - k) + 1)ak)] = 0 2
⇒ bh – hk + ak = 0
ak + bh = hk
Dividing both sides by hk, we getak + bh = 1 hk hk a + b = 1 h k Correct Option: A
We know that when three points are collinear than area of triangle is zero.
ar∆ = 
h 0 1 
1 a b 1 2 a b 1 ⇒ 1 [h(b - k) + 1)ak)] = 0 2
⇒ bh – hk + ak = 0
ak + bh = hk
Dividing both sides by hk, we getak + bh = 1 hk hk a + b = 1 h k
- What is the equation of line, which makes intercepts –5 and 2 on the x and y-axis respectively
-
View Hint View Answer Discuss in Forum
Here,
a = –5, b = 2
∴ Equation of line will bex + y = 1 a b ⇒ x + y = 1 - 5 2
⇒ 2x – 5y = – 10Correct Option: C
Here,
a = –5, b = 2
∴ Equation of line will bex + y = 1 a b ⇒ x + y = 1 - 5 2
⇒ 2x – 5y = – 10
- If the angle between two lines is π/4 and the slope of one of the lines is 1/2 , then the slope of other line will be
-
View Hint View Answer Discuss in Forum
Here,
θ = π 4
m1 = mm2 = 1 2
We know that
tan
⇒ 1 = 2m - 1 2 + m
→ 2 + m = 2m – 1
⇒ m = 3Correct Option: C
Here,
θ = π 4
m1 = mm2 = 1 2
We know that
tan
⇒ 1 = 2m - 1 2 + m
→ 2 + m = 2m – 1
⇒ m = 3
- What point on the x-axis are at a distance of 4 units from the line 3x – 4y – 5 = 0
-
View Hint View Answer Discuss in Forum
Let the co-ordinates of point p be (x, 0)
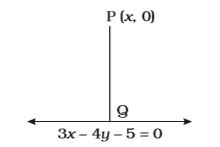
Also,
PQ = 4
⇒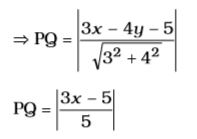
4 = 3x - 5 5
3 x – 5 = 20
3x = 25 x = 25 3∴ Co-ordinates are 
25 , 0 
3 Correct Option: D
Let the co-ordinates of point p be (x, 0)

Also,
PQ = 4
⇒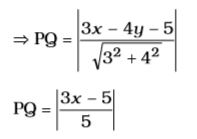
4 = 3x - 5 5
3 x – 5 = 20
3x = 25 x = 25 3∴ Co-ordinates are 
25 , 0 
3

