111. What will be the angle between the lines y – x – 7 = 0 and √3y – x + 6 = 0 ?

1. 1. θ = tan^–1(2 + √3)

   
   
   

   2. θ = tan^–1(2 - √3)

   
   
   

   3. θ = tan^–1(1 + √3)

   
   
   

   4. θ = tan^–1(1 - √3)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   We know that angle between the lines is
   

   tanθ =		m1 + m2
   		√1 + m1m2

   
   Here, Equation of line is y – x – 7 = 0
   ⇒ m₁ = 1
   similarly,
   

   m2 =	1
   	√3

   
   Now,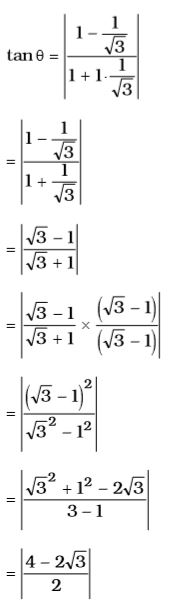
   
   tanθ = (2 - √3)
   θ = tan^–1(2 - √3)

   Correct Option: B

   We know that angle between the lines is
   

   tanθ =		m1 + m2
   		√1 + m1m2

   
   Here, Equation of line is y – x – 7 = 0
   ⇒ m₁ = 1
   similarly,
   

   m2 =	1
   	√3

   
   Now,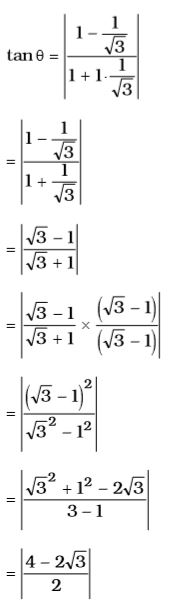
   
   tanθ = (2 - √3)
   θ = tan^–1(2 - √3)

---

112. Equation of line 3x + 2y – 5 = 0 can be written in intercept form as

1. 1. ⇒	x		+	y		= 1
      	5			5
      	3			2

   
   
   

   2. x	+	y	= 1
      5		3

   
   
   

   3. x	+	y	= 1
      2		5

   
   
   

   4. ⇒	x		-	y		= 1
      	5			5
      	3			2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   When a line cuts an intercept of a and b x-axis. Its equation will be
   

   	x	+	y
   	a		b

   
   ⇒ 3x + 2y – 5 = 0
   ⇒ 3x + 2y = 5
   Dividing by 5 on both sides, we get
   

   	3	x +	2	y = 1
   	5		5

   
   

   ⇒	x		+	y		= 1 (Desired Result)
   	5			5
   	2			2

   Correct Option: A

   When a line cuts an intercept of a and b x-axis. Its equation will be
   

   	x	+	y
   	a		b

   
   ⇒ 3x + 2y – 5 = 0
   ⇒ 3x + 2y = 5
   Dividing by 5 on both sides, we get
   

   	3	x +	2	y = 1
   	5		5

   
   

   ⇒	x		+	y		= 1 (Desired Result)
   	5			5
   	2			2

---

---

113. What is the distance between the parllel lines 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0 ?

1. 1. 2 units

   
   
   

   2. 5 units

   
   
   

   3. 6 units

   
   
   

   4. 65/17 units

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Distance between two parallel lines 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0 be d
   

   ⇒ d =		15x + 8y - 34
   		√15² + 8²

   
   We know that from second equation 15x + 8y = –31
   

   ⇒ d =		-31 - 34
   		√225 + 64

   
   

   =		-65
   		√289

   
   

   =		-65
   		17

   
   

   d =	65	units
   	17

   Correct Option: D

   Distance between two parallel lines 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0 be d
   

   ⇒ d =		15x + 8y - 34
   		√15² + 8²

   
   We know that from second equation 15x + 8y = –31
   

   ⇒ d =		-31 - 34
   		√225 + 64

   
   

   =		-65
   		√289

   
   

   =		-65
   		17

   
   

   d =	65	units
   	17

---

114. Find the ratio in which the line segment joining the points (1, 2) and (4, 6) is divided by point (2, 0).

1. 1. 1 : 2

   
   
   

   2. 2 : 1

   
   
   

   3. 1 : 4

   
   
   

   4. 2 : 3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let the ratio be k : 1
   
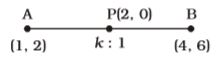
   Using internal section formula
   

   2 =	4 × k + 1 × 1
   	k + 1

   
   ⇒ 2(k + 1) = 4k + 1
   2k + 2 = 4k + 1
   –2k = –1
   

   k =	1
   	2

   
   and
   

   0 =	6 × k + 1 × 2
   	k + 1

   
   0 (k + 1) = 6k + 2
   6k = –2
   

   k =	- 1
   	3

   
   The value of k is not negative.
   ∴ Ratio will be 1 : 2

   Correct Option: A

   Let the ratio be k : 1
   
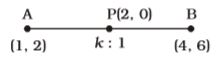
   Using internal section formula
   

   2 =	4 × k + 1 × 1
   	k + 1

   
   ⇒ 2(k + 1) = 4k + 1
   2k + 2 = 4k + 1
   –2k = –1
   

   k =	1
   	2

   
   and
   

   0 =	6 × k + 1 × 2
   	k + 1

   
   0 (k + 1) = 6k + 2
   6k = –2
   

   k =	- 1
   	3

   
   The value of k is not negative.
   ∴ Ratio will be 1 : 2

---

---

115. What is the distance of the point (2, 3) from the line 2x + 3y + 4 = 0 ?

1. 1. 15

      √13

   
   
   

   2. 16

      √13

   
   
   

   3. 17

      √13

   
   
   

   4. 8

      √13

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let the distance be d
   
   

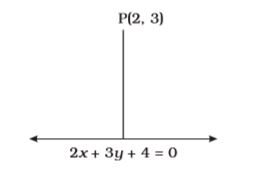
   ⇒ d =		2x + 3y + 4
   		√2² + 3²

   
   

   d(2,3) =		2 × 2 + 3 × 3 + 4
   		√13

   
   

   d(2,3) =		17		units
   		√13

   
   

   ⇒ d(2,3) =	17	units
   	√13

   Correct Option: C

   Let the distance be d
   
   

   ⇒ d =		2x + 3y + 4
   		√2² + 3²

   
   

   d(2,3) =		2 × 2 + 3 × 3 + 4
   		√13

   
   

   d(2,3) =		17		units
   		√13

   
   

   ⇒ d(2,3) =	17	units
   	√13

---