Algebra
- Area of the triangle formed by the graph of the straight lines x – y = 0, x + y = 2 and the x– axis is
-
View Hint View Answer Discuss in Forum
On putting x = 0 in x + y = 2,
0 + y = 2 Þ y = 2
∴ Point of intersection on y-axis = (0, 2)
Again,
putting y = 0 in x + y = 2, x = 2
∴ Point of intersection on x-axis = (2, 0)
x – y = 0 will pass through origin and be equally inclined to axes.
On putting x = y in x + y = 2, 2y = 2 ⇒ y = 1
∴ CD = 1 OA = 2Area of ∆ OAC = 1 × OA × CD = 1 × 2 × 1 = 1 sq. units 2 2 Correct Option: A
On putting x = 0 in x + y = 2,
0 + y = 2 Þ y = 2
∴ Point of intersection on y-axis = (0, 2)
Again,
putting y = 0 in x + y = 2, x = 2
∴ Point of intersection on x-axis = (2, 0)
x – y = 0 will pass through origin and be equally inclined to axes.
On putting x = y in x + y = 2, 2y = 2 ⇒ y = 1
∴ CD = 1 OA = 2Area of ∆ OAC = 1 × OA × CD = 1 × 2 × 1 = 1 sq. units 2 2
- The equations 3x + 4y = 10 – x + 2y = 0 have the solution (a,b). The value of a + b is
-
View Hint View Answer Discuss in Forum
3x + 4y = 10 ---(i)
– x + 2y = 0
⇒ x = 2y
∴ From equation (i),
3 × 2y + 4y = 10 Þ 10y = 10⇒ y = 10 = 1 10
∴ x = 2
∴ (a, b) = (2, 1)
∴ a + b = 2 + 1 = 3Correct Option: C
3x + 4y = 10 ---(i)
– x + 2y = 0
⇒ x = 2y
∴ From equation (i),
3 × 2y + 4y = 10 Þ 10y = 10⇒ y = 10 = 1 10
∴ x = 2
∴ (a, b) = (2, 1)
∴ a + b = 2 + 1 = 3
- The area in sq. unit. of the triangle formed by the graphs of x = 4, y = 3 and 3x + 4y = 12 is
-
View Hint View Answer Discuss in Forum
x = 4, a straight line parallel to y – axis.
y = 3, a straight line parallel to x – axis.
Putting x = 0 in 3x + 4y = 12, 3 × 0 + 4y = 12,⇒ 4y = 12 ⇒ y = 12 = 4 3
∴ Point of intersection on y – axis = (0, 4)
Again, putting y = 0 in 3x + 4y = 12, 3x + 4 × 0 = 12⇒ 3x = 12 ⇒ x = 12 = 4 3
∴ Point of intersection onx - axis = (4, 0)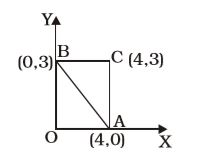
Area of ∎ OACB = OA × OB = 4 × 3 = 12 sq. unitsArea of ∆ OAB = 1 × OA × OB = 1 × 4 × 3 = 6 sq. units 2 2
∴ Area of ∆ABC = 12 – 6 = 6 sq. unitsCorrect Option: D
x = 4, a straight line parallel to y – axis.
y = 3, a straight line parallel to x – axis.
Putting x = 0 in 3x + 4y = 12, 3 × 0 + 4y = 12,⇒ 4y = 12 ⇒ y = 12 = 4 3
∴ Point of intersection on y – axis = (0, 4)
Again, putting y = 0 in 3x + 4y = 12, 3x + 4 × 0 = 12⇒ 3x = 12 ⇒ x = 12 = 4 3
∴ Point of intersection onx - axis = (4, 0)
Area of ∎ OACB = OA × OB = 4 × 3 = 12 sq. unitsArea of ∆ OAB = 1 × OA × OB = 1 × 4 × 3 = 6 sq. units 2 2
∴ Area of ∆ABC = 12 – 6 = 6 sq. units
- The graphs of x = a and y = b intersect at
-
View Hint View Answer Discuss in Forum
Point of intersection = (a, b)
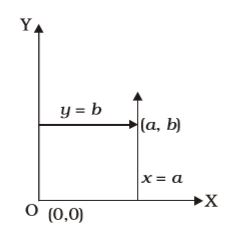
Correct Option: A
Point of intersection = (a, b)

- The straight line 2x + 3y = 12 passes through :
-
View Hint View Answer Discuss in Forum
Putting y = 0 in 4x + 3y = 12,
we get x = 3
Putting x = 0 in 4x + 3y = 12, we get, y = 4
Correct Option: B
Putting y = 0 in 4x + 3y = 12,
we get x = 3
Putting x = 0 in 4x + 3y = 12, we get, y = 4

