Algebra
- If the number of vertices, edges and faces of a rectangualr parallelopiped are denoted by v, e and f respectively, the value of (v– e+f )is
-
View Hint View Answer Discuss in Forum
Vertices of parallel to piped = v = 8
Edges = e = 12
Surfaces = f = 6
∴ v – e + f = 8 – 12 + 6 = 2Correct Option: B
Vertices of parallel to piped = v = 8
Edges = e = 12
Surfaces = f = 6
∴ v – e + f = 8 – 12 + 6 = 2
- The area of the triangle formed by the graphs of the equations x = 0, 2x+3y = 6 and x+y = 3 is :
-
View Hint View Answer Discuss in Forum

x = 0 ⇒ Equation of y – axis Putting x = 0 in 2x + 3y = 6
0 + 3y = 6 ⇒ y = 2
∴ Co-ordinates of point of intersection on y – axis
= (0, 2)
Again, putting y = 0, x = 3
∴ Point of intersection onx – axis = (3, 0)
In x + y = 3
Putting x = 0, y = 3
and on putting y = 0, x = 3∴ Required area = ∆OAC – ∆OAB = OCD = 1 × 3 × 3 - 1 × 3 × 2 2 2 = 9 - 6 = 3 2 2 2 = 1 1 sq. units 2 Correct Option: C

x = 0 ⇒ Equation of y – axis Putting x = 0 in 2x + 3y = 6
0 + 3y = 6 ⇒ y = 2
∴ Co-ordinates of point of intersection on y – axis
= (0, 2)
Again, putting y = 0, x = 3
∴ Point of intersection onx – axis = (3, 0)
In x + y = 3
Putting x = 0, y = 3
and on putting y = 0, x = 3∴ Required area = ∆OAC – ∆OAB = OCD = 1 × 3 × 3 - 1 × 3 × 2 2 2 = 9 - 6 = 3 2 2 2 = 1 1 sq. units 2
- If 5x + 9y = 5 and 125x³ + 729y3 = 120 then the vlaue of the product of x and y is
-
View Hint View Answer Discuss in Forum
5x + 9y = 5
On cubing both sides, (5x)³ + (9y)³ + 3 × 5x × 9y (5x + 9y) = (5)³
[∵ (a + b)³ = a³ + b³ + 3ab (a + b)]
⇒ 125x³ + 729y³ + 135xy × 5 = 125
⇒ 120 + 135 × 5xy = 125
⇒ 135 × 5xy = 125 – 120 = 5⇒ xy = 5 = 1 135 × 5 135 Correct Option: B
5x + 9y = 5
On cubing both sides, (5x)³ + (9y)³ + 3 × 5x × 9y (5x + 9y) = (5)³
[∵ (a + b)³ = a³ + b³ + 3ab (a + b)]
⇒ 125x³ + 729y³ + 135xy × 5 = 125
⇒ 120 + 135 × 5xy = 125
⇒ 135 × 5xy = 125 – 120 = 5⇒ xy = 5 = 1 135 × 5 135
- A point in the 4th quadrant is 6 unit away from x–axis and 7 unit away from y–axis. The point is at
-
View Hint View Answer Discuss in Forum
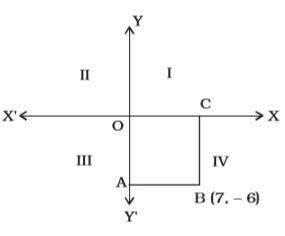
Correct Option: A

- The straight line y = 3x must pass through the point :
-
View Hint View Answer Discuss in Forum
y = 3x, passes through the origin (0, 0).
Correct Option: A
y = 3x, passes through the origin (0, 0).

