Algebra
- Sum of the factors of 4b²c² – (b² + c² – a²)² is :
-
View Hint View Answer Discuss in Forum
4b²c² – (b² + c² – a²)²
= (2bc)² – (b² + c² – a²)²
= (2bc + b² + c² –a²) (2bc – b² – c² + a²)
= {(b + c)² – a²} {a² – (b² + c² – 2bc)}
= (b + c + a) (b + c – a) {a² – (b–c)²}
= (b + c + a) (b + c – a) (a + b – c) (a – b + c)
∴ Required sum
= b + c + a + b + c – a + a + b – c + a – b + c
= 2 (a + b + c)Correct Option: B
4b²c² – (b² + c² – a²)²
= (2bc)² – (b² + c² – a²)²
= (2bc + b² + c² –a²) (2bc – b² – c² + a²)
= {(b + c)² – a²} {a² – (b² + c² – 2bc)}
= (b + c + a) (b + c – a) {a² – (b–c)²}
= (b + c + a) (b + c – a) (a + b – c) (a – b + c)
∴ Required sum
= b + c + a + b + c – a + a + b – c + a – b + c
= 2 (a + b + c)
- If (4a – 3)² = 0, then the value of 64a³ – 48a² + 12a + 13 is :
-
View Hint View Answer Discuss in Forum
(4a – 3)² = 0
⇒ 4a – 3 = 0
⇒ 4a = 3
⇒ a = 3/4
∴ 64a³ – 48a² + 12a + 13= 64 × 
3 
³ - 48 × 
3 
² + 12 × 3 + 13 4 4 4 = 64 × 27 - 48 × 9 + 9 + 13 64 16
= 27 – 27 + 22 = 22Correct Option: C
(4a – 3)² = 0
⇒ 4a – 3 = 0
⇒ 4a = 3
⇒ a = 3/4
∴ 64a³ – 48a² + 12a + 13= 64 × 
3 
³ - 48 × 
3 
² + 12 × 3 + 13 4 4 4 = 64 × 27 - 48 × 9 + 9 + 13 64 16
= 27 – 27 + 22 = 22
- .If x, y, z are the three factors of a³ – 7a – 6, then value of (x + y + z) will be
-
View Hint View Answer Discuss in Forum
a³ – 7a – 6 = 0
When a = –1
f(a) = –1 + 7 – 6 = 0
∴ (a + 1) is a factor.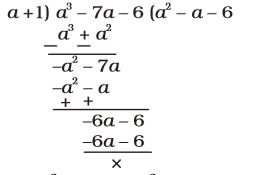
∴ a² – a – 6 = a² – 3a + 2a – 6
= a (a – 3) + 2 (a – 3)
= (a – 3) (a + 2)
∴ x + y + z
= a + 1 + a – 3 + a + 2 = 3aCorrect Option: A
a³ – 7a – 6 = 0
When a = –1
f(a) = –1 + 7 – 6 = 0
∴ (a + 1) is a factor.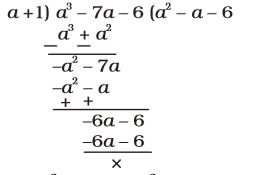
∴ a² – a – 6 = a² – 3a + 2a – 6
= a (a – 3) + 2 (a – 3)
= (a – 3) (a + 2)
∴ x + y + z
= a + 1 + a – 3 + a + 2 = 3a
-
If 
x + 1 
= -2, then the value of 
x7 + 1 
is : x x7
-
View Hint View Answer Discuss in Forum
x + 1 = -2 x ⇒ x² + 1 = -2 x
⇒ x² + 1 = – 2x
⇒ x² + 2x + 1 = 0
⇒ (x + 1)² = 0
⇒ x + 1 = 0 ⇒ x = –1∴ x7 + 1 = (-1)7 + 1 x7 (-1)7
= –1 –1 = – 2Correct Option: D
x + 1 = -2 x ⇒ x² + 1 = -2 x
⇒ x² + 1 = – 2x
⇒ x² + 2x + 1 = 0
⇒ (x + 1)² = 0
⇒ x + 1 = 0 ⇒ x = –1∴ x7 + 1 = (-1)7 + 1 x7 (-1)7
= –1 –1 = – 2
- If a² + b² + c² = 14 and a + b + c = 6, then the value of (ab + bc + ca) is,
-
View Hint View Answer Discuss in Forum
a² + b² + c² = 14 ..... (i)
a + b + c = 6
∴ (a + b + c)² = 6² = 36
⇒ a² + b² + c² + 2 (ab + bc + ca) = 36
⇒ 14 + 2 (ab + bc + ca) = 36
⇒ 2 (ab + bc + ca) = 36 – 14 = 22⇒ ab + bc + ca = 22 = 11 2 Correct Option: A
a² + b² + c² = 14 ..... (i)
a + b + c = 6
∴ (a + b + c)² = 6² = 36
⇒ a² + b² + c² + 2 (ab + bc + ca) = 36
⇒ 14 + 2 (ab + bc + ca) = 36
⇒ 2 (ab + bc + ca) = 36 – 14 = 22⇒ ab + bc + ca = 22 = 11 2

