Network Elements and the Concept of Circuit Easy Questions and Answers | Page - 8

Network Elements and the Concept of Circuit

The complex power in the circuit shown below will be—

1. 16.5 – 6.3°
1. 16.5 6.3°
1. 33 – 6.3°
1. 33 + 6.3°

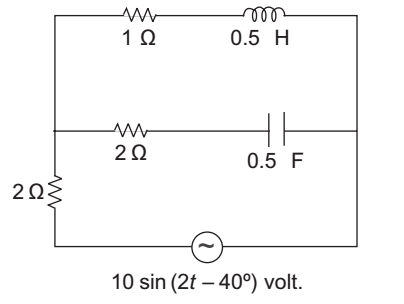
View Hint View Answer Discuss in Forum

Complex power is given by the relation
P = I V
given V = 10 sin (2t – 40°)V
for the given circuit

10 sin (2t – 40°) volt
Z _eq = 2 + 2 + 1 || (1 + 5s)
5s

= 3.02 ∠ 6.3° at ω = 2
I = V =
10 sin (2t – 40°)
Z_eq 3.02 – 6.3°

I = 3.3 sin (2t – 46.3°)
so, complex power
P = VI = V_m I_m cos φ
2

P = 10 × 3.3 ∠ – 6.3°
2

or P = 16.5 ∠ – 6.3° watts

Correct Option: A

Complex power is given by the relation
P = I V
given V = 10 sin (2t – 40°)V
for the given circuit

10 sin (2t – 40°) volt
Z _eq = 2 + 2 + 1 || (1 + 5s)
5s

= 3.02 ∠ 6.3° at ω = 2
I = V =
10 sin (2t – 40°)
Z_eq 3.02 – 6.3°

I = 3.3 sin (2t – 46.3°)
so, complex power
P = VI = V_m I_m cos φ
2

P = 10 × 3.3 ∠ – 6.3°
2

or P = 16.5 ∠ – 6.3° watts

The current I in the circuit will given by—

1. 5 amp
1. 1.2 amp
1. 2.4 amp
1. 0.6 amp

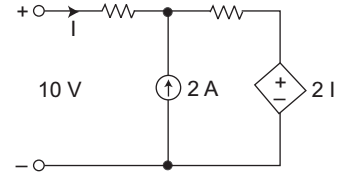
View Hint View Answer Discuss in Forum

Applying the KVL
10 = 1 I + 2 (I + 2) + 2 I
10 = I + 2 I + 4 + 2 I

10 – 4 = 5I
I = 6 = 1.2 amp.
5

Correct Option: B

Applying the KVL
10 = 1 I + 2 (I + 2) + 2 I
10 = I + 2 I + 4 + 2 I

10 – 4 = 5I
I = 6 = 1.2 amp.
5

The Thevenin equivalent of the given at terminal a – b will be—

1. None of these

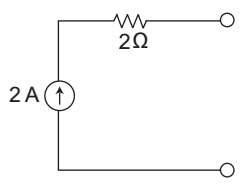
View Hint View Answer Discuss in Forum

Because we cannot connect a resistance in series with the current source.

Correct Option: D

Because we cannot connect a resistance in series with the current source.

Find the Thevenin voltage and resistance for the network shown below across the terminal A.B—

1. 27 V, 3 Ω
1. 18 V, 3 Ω
1. 27 V, 1 Ω
1. 18 V, 8 Ω

View Hint View Answer Discuss in Forum

Calculation for R_th
To calculate R_th when dependent source are taking into account for this, assume a imaginary source say 5 V is connected across terminal A and B and current produced by that current source is I then R_th is given by the relation.
R_th = 5/1
the equivalent circuit for calculating R_th is shown below:
5 = 2 V_x + I. 1 ....(i)
V_x = 1. I
5 = 2 I + I
I = 5 Ω
3

so, R_th = 5 = 3 Ω
5 / 3

Calculation for Vth:
Here the 3 A current source will drop across 1 Ω resistance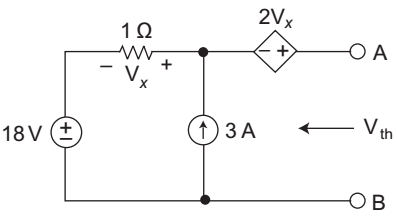

V_x = 3 × 1 = 3 V
or V_th = 2 V_x + V_x + 18
or V_th =3 V_x + 18 = 3 × 3 + 18 = 27 V

Correct Option: A

Calculation for R_th
To calculate R_th when dependent source are taking into account for this, assume a imaginary source say 5 V is connected across terminal A and B and current produced by that current source is I then R_th is given by the relation.
R_th = 5/1
the equivalent circuit for calculating R_th is shown below:
5 = 2 V_x + I. 1 ....(i)
V_x = 1. I
5 = 2 I + I
I = 5 Ω
3

so, R_th = 5 = 3 Ω
5 / 3

Calculation for Vth:
Here the 3 A current source will drop across 1 Ω resistance

V_x = 3 × 1 = 3 V
or V_th = 2 V_x + V_x + 18
or V_th =3 V_x + 18 = 3 × 3 + 18 = 27 V

The voltage of the source i.e. V_s, if i (t) = – 20 e^{– 2t}

1. 10 e_{– 2t}
1. 10 e_2t
1. 20 e_{– 2t}
1. 20 e_2t

View Hint View Answer Discuss in Forum

Given i (t) = – 20 e^{– 2t}
V (t) = – 20 e^{– 2t} × 1 = – 20 e^{– 2t}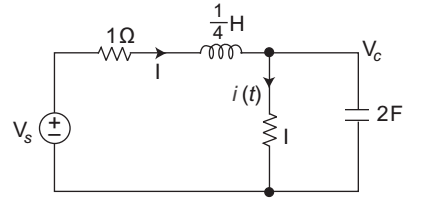

i_C = C dV (t)
dt

= 2. d (– 20 e– 2t)
dt

or i_C = 80 e^{– 2t}
I = i (t) + i _C = – 20 e^{– 2t} + 80 e^{– 2t}
= 60 e^{– 2t}
V_s = V_R + V_L + V (t)
= 1 × 60 e^{– 2t} + L d i + V (t)
dt

= 1 × 60 e_{– 2t} + 1
d 60 e_{– 2t} – 20 e_{– t}
4 dt

= 60 e_{– 2t} – 15 × 2 e_{– 2t} – 20 e_{– 2t}
= 60 e_{– 2t} – 30e_{– 2t} – 20 e_{– 2t}
= 10e_{– 2t}

Correct Option: A

Given i (t) = – 20 e^{– 2t}
V (t) = – 20 e^{– 2t} × 1 = – 20 e^{– 2t}

i_C = C dV (t)
dt

= 2. d (– 20 e– 2t)
dt

or i_C = 80 e^{– 2t}
I = i (t) + i _C = – 20 e^{– 2t} + 80 e^{– 2t}
= 60 e^{– 2t}
V_s = V_R + V_L + V (t)
= 1 × 60 e^{– 2t} + L d i + V (t)
dt

= 1 × 60 e_{– 2t} + 1
d 60 e_{– 2t} – 20 e_{– t}
4 dt

= 60 e_{– 2t} – 15 × 2 e_{– 2t} – 20 e_{– 2t}
= 60 e_{– 2t} – 30e_{– 2t} – 20 e_{– 2t}
= 10e_{– 2t}