Network Elements and the Concept of Circuit

Network Elements and the Concept of Circuit

Easy Questions

Network Theory

Network Elements and the Concept of Circuit
Network theory miscellaneous
  1. Calculate the value of R in ohms under maximum power transfer condition for the circuit shown below—










  1. View Hint View Answer Discuss in Forum


    From above figure, if we apply maximum power transfer theorem, then
    RL = Rth = 20|| R

    or RL =
    20R
    20 + R

    or 16 =
    20R
    20 + R

    or R = 80Ω
    However, the maximum power will transfer if and only if R = 0, so that there is no voltage drop in internal resistances. Therefore alternative (B) is the correct choice.

    Correct Option: B


    From above figure, if we apply maximum power transfer theorem, then
    RL = Rth = 20|| R

    or RL =
    20R
    20 + R

    or 16 =
    20R
    20 + R

    or R = 80Ω
    However, the maximum power will transfer if and only if R = 0, so that there is no voltage drop in internal resistances. Therefore alternative (B) is the correct choice.

  1. For the circuit arrangement shown below. Calculate the value of R under maximum power transfer condition—










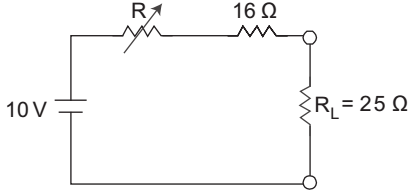
  1. View Hint View Answer Discuss in Forum


    From above figure it is clear that under maximum power transfer condition R should be equals to zero ohm. Hence alternative (C) is the correct choice.

    Correct Option: C


    From above figure it is clear that under maximum power transfer condition R should be equals to zero ohm. Hence alternative (C) is the correct choice.

  1. The power delivered by element 3 in figure shown below is—










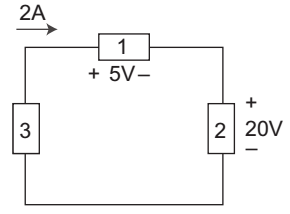
  1. View Hint View Answer Discuss in Forum

    From given figure

    Power absorbed by element 1 & 2 = [2 × 5 + 2 × 20] = – 50W
    Thus the element 3 absorbs 50W of power or, equivalently, delivers 50 W.

    Correct Option: B

    From given figure

    Power absorbed by element 1 & 2 = [2 × 5 + 2 × 20] = – 50W
    Thus the element 3 absorbs 50W of power or, equivalently, delivers 50 W.

  1. Calculate the equivalent resistance at terminal A and B—










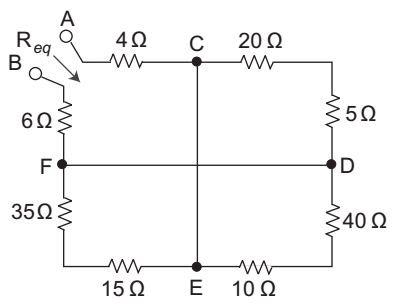
  1. View Hint View Answer Discuss in Forum


    where, RCD or REF = 25 || 50 || 50 = 12.5 Ω
    RAB = 4 + 6 + 12.5 = 22.5 Ω
    Hence alternative (B) is the correct choice

    Correct Option: B


    where, RCD or REF = 25 || 50 || 50 = 12.5 Ω
    RAB = 4 + 6 + 12.5 = 22.5 Ω
    Hence alternative (B) is the correct choice

  1. D.C. component of the waveform shown below is—










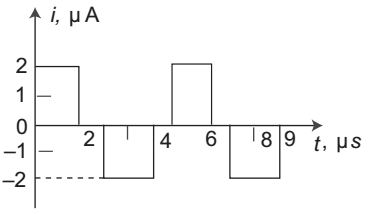
  1. View Hint View Answer Discuss in Forum

    D.C. component =
    1
    		 f(t) dt
    TT

    =
    1
    		12 dt +20.dt +4– 2 dt +50 dt
    50114

    =
    1
    		[2 + 0 + (– 8 + 4) + 0] µA
    5

    =
    –2
    		= – 0.4 µA
    5

    Correct Option: B

    D.C. component =
    1
    		 f(t) dt
    TT

    =
    1
    		12 dt +20.dt +4– 2 dt +50 dt
    50114

    =
    1
    		[2 + 0 + (– 8 + 4) + 0] µA
    5

    =
    –2
    		= – 0.4 µA
    5