111. Find the rms value of the wave shown below—.
     
     
     

1. 1. Vm
      3

   
   
   

   2. 2Vm
      3

   
   
   

   3. Vm
      2

   
   
   

   4. Vm
      2

      
      

   
   
   

---

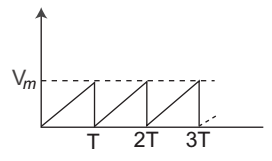
1. View Hint View Answer Discuss in Forum

   Remember always rms value of given periodic wave is
   

   	Vm	.
   	√3

   
   

   Correct Option: A

   Remember always rms value of given periodic wave is
   

   	Vm	.
   	√3

   
   

---

112. The number of branches and nodes in the graph are—
     
     
     

1. 1. 5, 10

   
   
   

   2. 10, 5

   
   
   

   3. 10, 10

   
   
   

   4. 6, 10

   
   
   

---

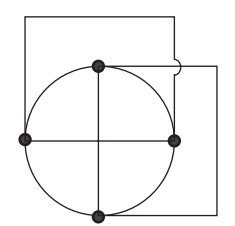
1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: B

   NA

---

---

113. In the figure the transformer is ideal with adjustable turns ratio N₂ / N₁ . The turns ratio N₂ / N₁ for maximum power transfer to the load is—
     
     
     

1. 1. 1: 1

   
   
   

   2. 100: 1

   
   
   

   3. 1: 100

   
   
   

   4. 1000: 1

   
   
   

---

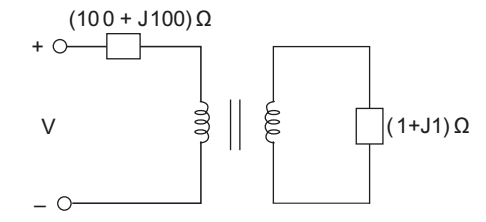
1. View Hint View Answer Discuss in Forum

   As given that transformer is ideal it means
   I₁ = I₂ = I (say)
   so, V₁ = I₁ (100 + J100) = I (100+ J100) = 100 I₁ (J+ 1)
   and V₂ = I₂ (1 + J) = I (1 + J)
   

   So,		V2	=	N2	=	(1 + J) I	=	1
   		V1		N1		100! (1 + J)		100

   
   

   	N2	= 1: 100
   	N1

   Correct Option: C

   As given that transformer is ideal it means
   I₁ = I₂ = I (say)
   so, V₁ = I₁ (100 + J100) = I (100+ J100) = 100 I₁ (J+ 1)
   and V₂ = I₂ (1 + J) = I (1 + J)
   

   So,		V2	=	N2	=	(1 + J) I	=	1
   		V1		N1		100! (1 + J)		100

   
   

   	N2	= 1: 100
   	N1

---

114. A single phase transformer is connected as shown in fig. when a voltage of 100 V (rms) was applied across AB, the voltmeter connected across AC measured 100 V (rms). The turns ratio N₁: N₂ is—
     
     
     

1. 1. 1: 1

   
   
   

   2. 1: 2

   
   
   

   3. 2: 1

   
   
   

   4. 4: 1

   
   
   

---

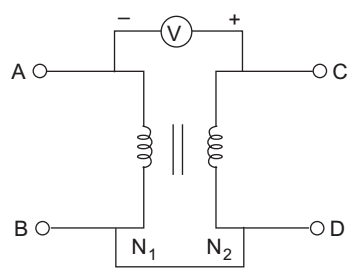
1. View Hint View Answer Discuss in Forum

   Since the reading of voltameter is 100 Vrms it means the output voltage is equal to
   V₂ = 100 + 100 = 200 V_rms
   

   So,		V2	=	N2	=	200	=	2
   		V1		N1		100		1

   
   or N₁: N₂ = 1: 2

   Correct Option: B

   Since the reading of voltameter is 100 Vrms it means the output voltage is equal to
   V₂ = 100 + 100 = 200 V_rms
   

   So,		V2	=	N2	=	200	=	2
   		V1		N1		100		1

   
   or N₁: N₂ = 1: 2

---

---

115. A capacitor is charged by a square wave current source, the voltage across the capacitor is—

1. 1. a square wave

   
   
   

   2. a triangular wave

   
   
   

   3. a step function

   
   
   

   4. zero

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Voltage across the capacitor is given by the relation
   

   V =	1	∫ i dt Where, i = square wave
   	C

   
   since the integration of square wave gives triangular wave so the voltage across the capacitor will be like a triangular wave.

   Correct Option: B

   Voltage across the capacitor is given by the relation
   

   V =	1	∫ i dt Where, i = square wave
   	C

   
   since the integration of square wave gives triangular wave so the voltage across the capacitor will be like a triangular wave.

---