Network Elements and the Concept of Circuit

Network Elements and the Concept of Circuit

Easy Questions

Network Theory

Network Elements and the Concept of Circuit
Network theory miscellaneous
  1. What will b e the value of
    diL
    		for given figure?
    dt








  1. View Hint View Answer Discuss in Forum

    As we know that

    VL = L
    diL
    dt

    – 2 = 2
    diL
    dt

    so,
    diL
    		= –1 H/sec
    dt

    Correct Option: B

    As we know that

    VL = L
    diL
    dt

    – 2 = 2
    diL
    dt

    so,
    diL
    		= –1 H/sec
    dt

  1. What will be the voltage across the capacitor at t = 0+ for given figure?








  1. View Hint View Answer Discuss in Forum

    In order to find the voltage across capacitor at t = 0+ the circuit becomes

    Note: In this type of question when both C and L are connected in the circuit, we can't apply general formula, because it is very difficult to calculate the time constant τ so we go for tricky method.
    Apply KCL at node (1)

    V - 6
    		=
    V - 0
    		 + 3 = 0
    42

    V
    		+
    V
    		=
    - 3
    422

    or V = – 2 V.

    Correct Option: B

    In order to find the voltage across capacitor at t = 0+ the circuit becomes

    Note: In this type of question when both C and L are connected in the circuit, we can't apply general formula, because it is very difficult to calculate the time constant τ so we go for tricky method.
    Apply KCL at node (1)

    V - 6
    		=
    V - 0
    		 + 3 = 0
    42

    V
    		+
    V
    		=
    - 3
    422

    or V = – 2 V.

  1. Switch S in position (1) for long time and moved to position (2) at t = 0 sec. obtain at t = 0+ the value of i L (0+)—










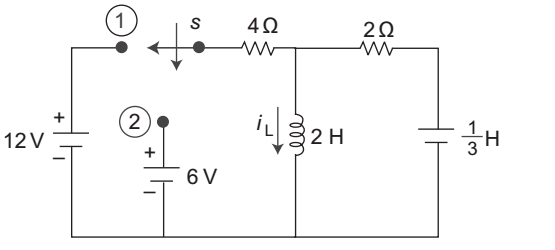
  1. View Hint View Answer Discuss in Forum

    At steady state the equivalent circuit becomes

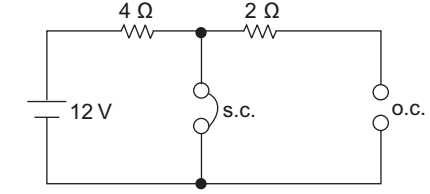
    i (0–) =i (0+) =
    12
    		= 3 amp.
    4

    Correct Option: A

    At steady state the equivalent circuit becomes

    i (0–) =i (0+) =
    12
    		= 3 amp.
    4

  1. What will be the value of i (t) for t > 0, the circuit shown in figure?










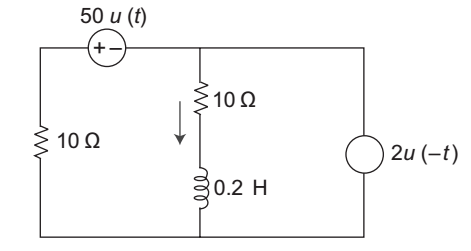
  1. View Hint View Answer Discuss in Forum

    For t > 0 2 u (– t) ⇒ not exist while 50 u (t) → exist, so the circuit becomes like

    i (∞) = -
    50
    		= – 2.5 amp.
    20

    i (0–) = i (0+) = 1 amp.
    τ =
    L
    		=
    .2
    		= .01
    R20

    we know that
    i (t)=[i (0) – i (∞)] e –t / τ + i (∞) .....(i)
    on putting the values in equation (i), we get
    i (t) = [1 – (– 2.5)] e – t .01 – 2.5

    Correct Option: A

    For t > 0 2 u (– t) ⇒ not exist while 50 u (t) → exist, so the circuit becomes like

    i (∞) = -
    50
    		= – 2.5 amp.
    20

    i (0–) = i (0+) = 1 amp.
    τ =
    L
    		=
    .2
    		= .01
    R20

    we know that
    i (t)=[i (0) – i (∞)] e –t / τ + i (∞) .....(i)
    on putting the values in equation (i), we get
    i (t) = [1 – (– 2.5)] e – t .01 – 2.5

  1. The value of i (t) < 0 is given by the relation for the circuit shown below—










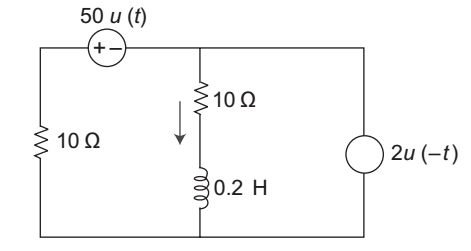
  1. View Hint View Answer Discuss in Forum

    For t < 0, 50 u (t) → not exist, so the circuit becomes like

    i L (0–) = i L (0+) = 2 ×
    10
    		= 1 amp.
    10 + 10

    so, i (t) = 1 u (– t)

    Correct Option: D

    For t < 0, 50 u (t) → not exist, so the circuit becomes like

    i L (0–) = i L (0+) = 2 ×
    10
    		= 1 amp.
    10 + 10

    so, i (t) = 1 u (– t)