Network Elements and the Concept of Circuit

Network Elements and the Concept of Circuit

Easy Questions

Network Theory

Network Elements and the Concept of Circuit
Network theory miscellaneous
  1. For a network of 11 branches and 6 nodes, what is the number of independent loops?








  1. View Hint View Answer Discuss in Forum

    Number of loop,
    L = b – n + 1
    = 11 – 6 + 1 = 6
    Where, b = No. of branches
    n = No. of nodes.

    Correct Option: C

    Number of loop,
    L = b – n + 1
    = 11 – 6 + 1 = 6
    Where, b = No. of branches
    n = No. of nodes.

  1. Consider the following circuit:

    For what value of, the circuit shown above exhibits unity power factor?








  1. View Hint View Answer Discuss in Forum


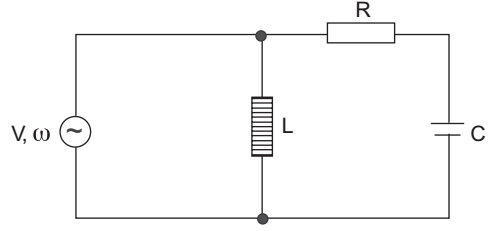
    For unity power factor: Circuit should have pure resistance. ...
    ∵ This condition will arise when, resonance takes place. When,
    Y = G + JB and B = 0

    Y =
    1
    		 +
    1
    R – JXCJXL


    or Y =
    R + JXC
    		 -
    1
    R2 + XC2XL


    or Y =
    R
    		+ J
    XC
    		 -
    1
    R2 + XC2R2 + XC2XL

    For resonance
    XC
    		 =
    1
    R2 + XC2XL

    XC XL = R2 + XC2
    L
    		= R2 +
    1
    Cω2C2

    L
    		 - R2 =
    1
    Cω2C2

    L – R2C
    		 =
    1
    Cω2C2

    ω2 =
    1
    ω2C2

    ω2 =
    1
    LC – R2C2


    or ω =
    1
    √LC – R²C²

    Correct Option: B


    For unity power factor: Circuit should have pure resistance. ...
    ∵ This condition will arise when, resonance takes place. When,
    Y = G + JB and B = 0

    Y =
    1
    		 +
    1
    R – JXCJXL


    or Y =
    R + JXC
    		 -
    1
    R2 + XC2XL


    or Y =
    R
    		+ J
    XC
    		 -
    1
    R2 + XC2R2 + XC2XL

    For resonance
    XC
    		 =
    1
    R2 + XC2XL

    XC XL = R2 + XC2
    L
    		= R2 +
    1
    Cω2C2

    L
    		 - R2 =
    1
    Cω2C2

    L – R2C
    		 =
    1
    Cω2C2

    ω2 =
    1
    ω2C2

    ω2 =
    1
    LC – R2C2


    or ω =
    1
    √LC – R²C²

  1. Use the data of figure (a). The current i in the circuit of figure (b)—








  1. View Hint View Answer Discuss in Forum

    This is a reciprocal and linear network. According to reciprocity theorem which states ‘‘Two loops A and B of a network N and if an ideal voltage source E in the loop A produces a current I in loop B, then interchanging positions an identical source in loop B produces the same current in loop A’’. Since network is linear, principle of homogeneity holds and so when voltage source is doubled current will also doubles.

    Correct Option: D

    This is a reciprocal and linear network. According to reciprocity theorem which states ‘‘Two loops A and B of a network N and if an ideal voltage source E in the loop A produces a current I in loop B, then interchanging positions an identical source in loop B produces the same current in loop A’’. Since network is linear, principle of homogeneity holds and so when voltage source is doubled current will also doubles.

  1. For the circuit shown below, the Thevenin’s resistance across the terminal A and B is—








  1. View Hint View Answer Discuss in Forum


    Since here dependent source is connected in the circuit therefore Thevenin’s resistance, Rth is given by

    Rth =
    VOC
    ISC

    Where,
    VOC = Open circuit voltage
    ISC = Short circuit current
    Calculation of ISC: Equivalent circuit is shown below.
    ISC =
    5V
    		= 2.5 mA
    2kΩ


    Calculation of VOC: Equivalent circuit is shown below.

    5 = 2I + 3 VAB + 1. I1
    or 5 = 6 I1 + 2I2 ....(i)
    and 5 = 2I + 2I2
    or 5 = 4I1 + 2I1 ....(ii)
    From equations (i) and (ii)
    I2 = 2I1
    and
    I1 = 0.5 mA
    VAB = VOC = I1 × 1kΩ
    = 0.5 mA × 1 kΩ
    = 0.5 V
    Now,
    Rth =
    VOC
    		=
    0.5
    ISC2.5 × 10–3

    or
    Rth = 0.2 kΩ.

    Correct Option: B


    Since here dependent source is connected in the circuit therefore Thevenin’s resistance, Rth is given by

    Rth =
    VOC
    ISC

    Where,
    VOC = Open circuit voltage
    ISC = Short circuit current
    Calculation of ISC: Equivalent circuit is shown below.
    ISC =
    5V
    		= 2.5 mA
    2kΩ


    Calculation of VOC: Equivalent circuit is shown below.

    5 = 2I + 3 VAB + 1. I1
    or 5 = 6 I1 + 2I2 ....(i)
    and 5 = 2I + 2I2
    or 5 = 4I1 + 2I1 ....(ii)
    From equations (i) and (ii)
    I2 = 2I1
    and
    I1 = 0.5 mA
    VAB = VOC = I1 × 1kΩ
    = 0.5 mA × 1 kΩ
    = 0.5 V
    Now,
    Rth =
    VOC
    		=
    0.5
    ISC2.5 × 10–3

    or
    Rth = 0.2 kΩ.

  1. Two two-part networks are connected in parallel. The combination is to be represented as a single two-port network. The parameters of this network are obtained by addition of the individual—








  1. View Hint View Answer Discuss in Forum

    When the two-port networks are connected in parallel. The equivalent parameters obtained by addition of the individual with the help of y-parameters.

    Correct Option: C

    When the two-port networks are connected in parallel. The equivalent parameters obtained by addition of the individual with the help of y-parameters.