Network Elements and the Concept of Circuit
- Extra element present in the given circuit—
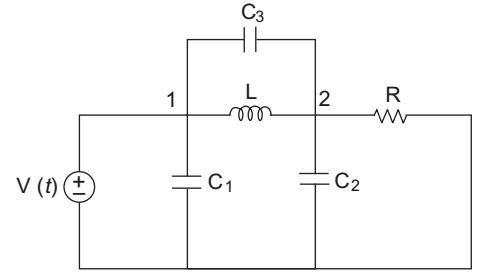
-
View Hint View Answer Discuss in Forum
The extra element present in the given circuit is C1. Because voltage at node 1 is independent of the capacitor C1.
Correct Option: A
The extra element present in the given circuit is C1. Because voltage at node 1 is independent of the capacitor C1.
- For the figure given below which of these sets of E, R and C value will ensure that the state equation dVc / dt = 1.25 VC + 2 is valid—
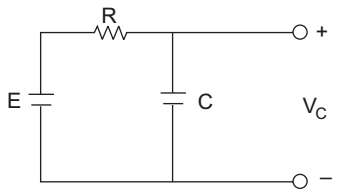
-
View Hint View Answer Discuss in Forum
We know that current across capacitor is given by the relation
i = C dv ....(i) dt
Applying KVL to the given circuit
E = iR + VC
E = RC dVC + VC dt E - VC = dVC .....(ii) RC RC dt
on comparing equation (ii) with the given standard equationdVC = 1.25 VC + 2 ....(iii) dt
from equations (i), (ii) and (iii), we getE = 2 and VC = 1.25
VC ⇒ RC =1C .....(ii) RC RC 1.25 E = 2RC = 2 × 1 = 1.6 1.25 RC = 1 = 0.8 given in option (B) and (C) 1.25
Correct Option: E
We know that current across capacitor is given by the relation
i = C dv ....(i) dt
Applying KVL to the given circuit
E = iR + VC
E = RC dVC + VC dt E - VC = dVC .....(ii) RC RC dt
on comparing equation (ii) with the given standard equationdVC = 1.25 VC + 2 ....(iii) dt
from equations (i), (ii) and (iii), we getE = 2 and VC = 1.25
VC ⇒ RC =1C .....(ii) RC RC 1.25 E = 2RC = 2 × 1 = 1.6 1.25 RC = 1 = 0.8 given in option (B) and (C) 1.25
- The r.m.s. value for the given wave is given by—
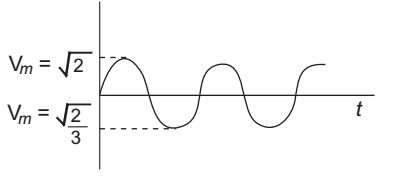
-
View Hint View Answer Discuss in Forum
rms value of the complete waveform
= 1 √(rms value of the Ist waveform)² + (rms value of the second waveform)² √2 = 1 √ 
√Vm 
2 + 
√Vm 
2 √2 √2 √2 = 1 √ 
√2 
2 + 
√2 
2 √2 √2 3√2 
∵ vm1 = √2 
vm2 = √2 3 = 1 √1 + ⅑ √2
= √10/18Correct Option: A
rms value of the complete waveform
= 1 √(rms value of the Ist waveform)² + (rms value of the second waveform)² √2 = 1 √ 
√Vm 
2 + 
√Vm 
2 √2 √2 √2 = 1 √ 
√2 
2 + 
√2 
2 √2 √2 3√2 
∵ vm1 = √2 
vm2 = √2 3 = 1 √1 + ⅑ √2
= √10/18
- Calculate the rms value of the given wave—
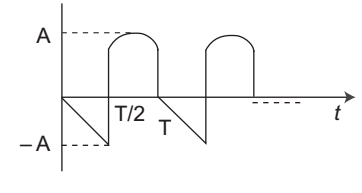
-
View Hint View Answer Discuss in Forum
rms value of the given waveform
= 1 √(rms value of 1st waveform)2 + (rms value of 2nd waveform)2 √2 = 1 √(A / √3 2) + √(A / √2 2) √2 = 1 √(A2 / 3) + √(A2 / 2) √2
= A√5 / 12Correct Option: B
rms value of the given waveform
= 1 √(rms value of 1st waveform)2 + (rms value of 2nd waveform)2 √2 = 1 √(A / √3 2) + √(A / √2 2) √2 = 1 √(A2 / 3) + √(A2 / 2) √2
= A√5 / 12
- Calculate the rms value of the given wave—
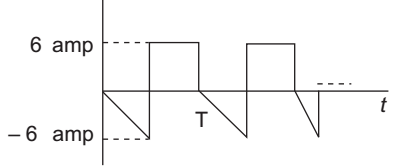
-
View Hint View Answer Discuss in Forum
rms value of the given wave
= 1 √(rms value of 1st waveform)2 + (rms value of 2nd waveform)2 √2 = 1 √(6 / √3)2 + (6)2 √2 = 1 √36 / 3 + (36) = √24 = 2 √6 √2
Correct Option: A
rms value of the given wave
= 1 √(rms value of 1st waveform)2 + (rms value of 2nd waveform)2 √2 = 1 √(6 / √3)2 + (6)2 √2 = 1 √36 / 3 + (36) = √24 = 2 √6 √2
-