Network Elements and the Concept of Circuit

Network Elements and the Concept of Circuit

Easy Questions

Network Theory

Network Elements and the Concept of Circuit
Network theory miscellaneous
  1. What will be the value of
    dVC
    		for given figure?
    dt








  1. View Hint View Answer Discuss in Forum

    We know that

    ic = C
    dVC
    dt

    = – 3 V/sec.

    Correct Option: A

    We know that

    ic = C
    dVC
    dt

    = – 3 V/sec.

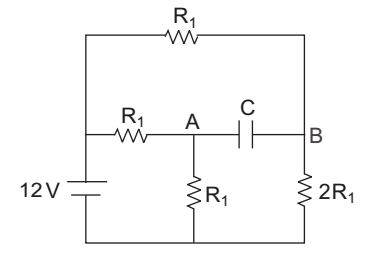
  1. Find VC (0+) for the circuit—










  1. View Hint View Answer Discuss in Forum

    Applying potential divider rule

    VA = 12.
    R1
    		= 6V
    R1 + R1

    VB = 12.
    2R1
    		= 8V
    2R1 + R1

    VC (0+) = VB – VA = 8 – 6 = 2 V

    Correct Option: A

    Applying potential divider rule

    VA = 12.
    R1
    		= 6V
    R1 + R1

    VB = 12.
    2R1
    		= 8V
    2R1 + R1

    VC (0+) = VB – VA = 8 – 6 = 2 V

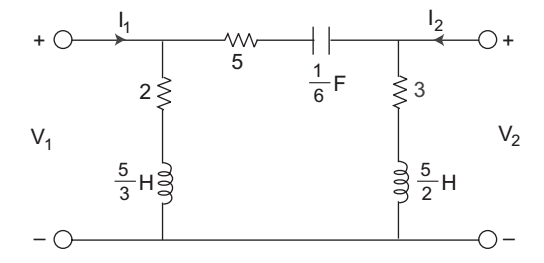
  1. The Y11-parameters for the given network shown below are—










  1. View Hint View Answer Discuss in Forum

    We given network

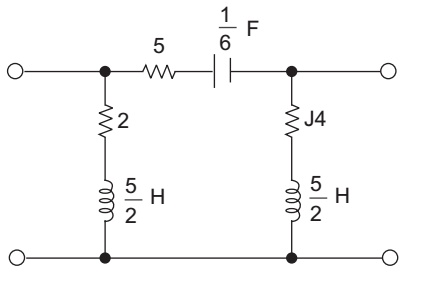
    Compare this network with standard network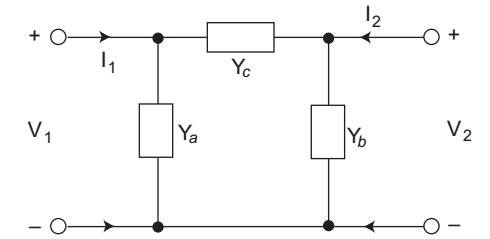

    Ya =
    1
    		+
    1
    		=
    1
    		+
    3

    25 / 2 x (s)25s / 3

    Yb =
    1
    		+
    1
    		=
    1
    		+
    2

    35 / 2 x (s)35s / 3

    Yc =
    1
    		+
    1
    		=
    1
    		 + 6s
    51 / 6 s5

    Y11 = Ya + Yc =
    1
    		+
    3
    		+
    1
    		 + 6s
    25s5

    Correct Option: A

    We given network

    Compare this network with standard network

    Ya =
    1
    		+
    1
    		=
    1
    		+
    3

    25 / 2 x (s)25s / 3

    Yb =
    1
    		+
    1
    		=
    1
    		+
    2

    35 / 2 x (s)35s / 3

    Yc =
    1
    		+
    1
    		=
    1
    		 + 6s
    51 / 6 s5

    Y11 = Ya + Yc =
    1
    		+
    3
    		+
    1
    		 + 6s
    25s5

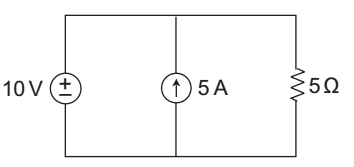
  1. The value of current I flowing in 5 Ω resistor in the figure, is—










  1. View Hint View Answer Discuss in Forum

    Apply the superposition theorem in the given circuit
    Case I. When 10 V source is treated 5 A current source is replaced by their internal resistance (i.e. open circuited)

    Now, 10 = 5 I ⇒ 1 = 2 Amp.
    Case II. When current source (5 A) is treated and voltage source (10 V) S.C. the circuit becomes

    According to the current division rule I will be zero so, the net current I = 2 amp.

    Correct Option: B

    Apply the superposition theorem in the given circuit
    Case I. When 10 V source is treated 5 A current source is replaced by their internal resistance (i.e. open circuited)

    Now, 10 = 5 I ⇒ 1 = 2 Amp.
    Case II. When current source (5 A) is treated and voltage source (10 V) S.C. the circuit becomes

    According to the current division rule I will be zero so, the net current I = 2 amp.

  1. The time constant of the network shown in the figure is—










  1. View Hint View Answer Discuss in Forum

    τ = R eq. C eq Ceq = C + C = 2C

    so, time constant Req =
    2R . 2R
    		= R
    2R + 2R

    τ = R. 2C = 2RC

    Correct Option: A

    τ = R eq. C eq Ceq = C + C = 2C

    so, time constant Req =
    2R . 2R
    		= R
    2R + 2R

    τ = R. 2C = 2RC