Network Elements and the Concept of Circuit Easy Questions and Answers | Page - 29

Network Elements and the Concept of Circuit

The Laplace transform of (t ₂ – 2t) u (t – 1) is—

1. = 2 e^{–s^–} 2 e^{– s}
  s³ s²
1. = 2 e^–s⁺ 2 e^{– s}
  s³ s²
1. = 2 e^{–2s^-} 1 e^{– s}
  s³ s
1. None of these

View Hint View Answer Discuss in Forum

(t ² – 2 t) u (t – 1) can be written as in the form
= (t – 1)² u (t – 1) – u (t – 1) taking Laplace transform

= 2 e^{–s^–} e^–s
s³ s

Correct Option: D

(t ² – 2 t) u (t – 1) can be written as in the form
= (t – 1)² u (t – 1) – u (t – 1) taking Laplace transform

= 2 e^{–s^–} e^–s
s³ s

For the circuit shown below in the figure, the voltage V₀ is—

1. 2 V
1. 1 V
1. – 1 V
1. None of these

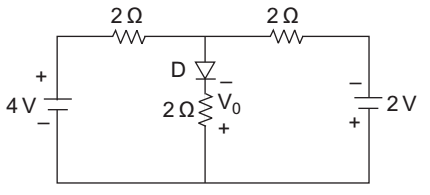
View Hint View Answer Discuss in Forum

This question can be easily solve by using superposition theorem.
Case I. Take 4V source the circuit becomes neglecting the voltage drop across diode by applying potential divider method voltage drop across AB

V_AB = 2 x 4 = 2V
2 + 2

Case II. Take 2 V source the circuit becomes due to 2V source there will be no current flowing through the terminal AB because diode becomes reverse bias under this situation.

Hence there will be no voltage drop across terminal AB due to this voltage source.
So net voltage = 2 V
But V₀ = – 2V (∵ as sign are opposite)
so, alternative (D) is the correct answer.

Correct Option: D

This question can be easily solve by using superposition theorem.
Case I. Take 4V source the circuit becomes neglecting the voltage drop across diode by applying potential divider method voltage drop across AB

V_AB = 2 x 4 = 2V
2 + 2

Case II. Take 2 V source the circuit becomes due to 2V source there will be no current flowing through the terminal AB because diode becomes reverse bias under this situation.

Hence there will be no voltage drop across terminal AB due to this voltage source.
So net voltage = 2 V
But V₀ = – 2V (∵ as sign are opposite)
so, alternative (D) is the correct answer.

The voltage V in the given figure is—

1. 2 V
1. 4 V
  3
1. 4 V
1. 8 V

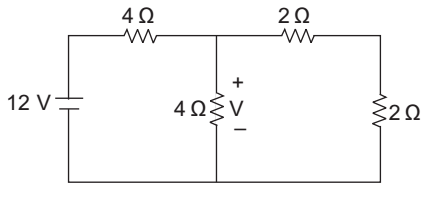
View Hint View Answer Discuss in Forum

In order to calculate the voltage across 4 Ω resistor, first we will calculate the current in 4 resistor due to voltage source, due to finding this calculate I as shown in the figure.

I = V
R_eq

R _eq = 4 + 4 || (2 + 2) = 4 + 2 = 6 Ω
so, I = 12 = 2 amp.
6

Now, the current in branch AB

= I × 4 =
2 x 4 = 1 amp.
4 + 4 8

so, voltage drop across 4 Ω = 1 × 4 = 4 V

Correct Option: C

In order to calculate the voltage across 4 Ω resistor, first we will calculate the current in 4 resistor due to voltage source, due to finding this calculate I as shown in the figure.

I = V
R_eq

R _eq = 4 + 4 || (2 + 2) = 4 + 2 = 6 Ω
so, I = 12 = 2 amp.
6

Now, the current in branch AB

= I × 4 =
2 x 4 = 1 amp.
4 + 4 8

so, voltage drop across 4 Ω = 1 × 4 = 4 V

The voltage across the 1 kΩ resistor between A and B of the network shown in the given figure is— 10 V 2k Ω 2k Ω 2A 1k Ω A B (A) (B) 14 3 V (C) (D) 26 3 V

1. 12 V
1. 14 V
  3
1. 10 V
1. 26 V
  3

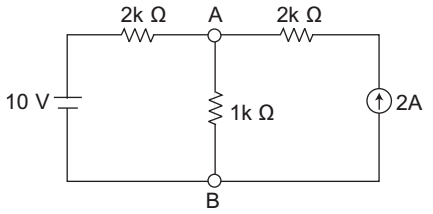
View Hint View Answer Discuss in Forum

In order to calculate the voltage drop between A and B Apply Superposition theorem.

Case I. When 10 V source is taken circuit becomes b

V_AB = 1 . 10 =
10 V (say V₁)
1 + 2 3

Case II. When current source is taken circuit becomes current in branch AB

I = 2 × 2 =
4 amp.
2 + 1 3

Voltage drop across AB = 4 × 1 =
4 V (say V₂)
3 3

Net voltage drop between

A and B = V₁ + V₂ = 10 +
4 =
14 V
3 3 3

Correct Option: B

In order to calculate the voltage drop between A and B Apply Superposition theorem.

Case I. When 10 V source is taken circuit becomes b

V_AB = 1 . 10 =
10 V (say V₁)
1 + 2 3

Case II. When current source is taken circuit becomes current in branch AB

I = 2 × 2 =
4 amp.
2 + 1 3

Voltage drop across AB = 4 × 1 =
4 V (say V₂)
3 3

Net voltage drop between

A and B = V₁ + V₂ = 10 +
4 =
14 V
3 3 3

In the figure below, the voltage across the 18 ohm resistor is 90 volts. What is the total voltage across the combined circuit at terminal E and F?

1. 125 V
1. 16 V
1. 24 V
1. 40 V

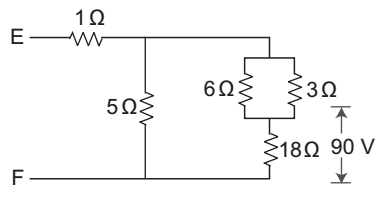
View Hint View Answer Discuss in Forum

In the given circuit voltage across 18 Ω is 90 V: so, I across 18 Ω will be
I = 90 = 5 amp.
18

Voltage drop across AB = 5. 3 || 6 = 5 × 2 = 10 V
Voltage drop across AC = 90 + 10 = 100 V
Current in 5 Ω resistor = 100 = 20 amp.
5

so, Current flowing through 1 Ω resistor = 20 + 5 = 25 amp.
Voltage drop across 1 Ω = 25 × 1 = 25 V
so, voltage drop across the terminal E and F
= 25 + 100 = 125 V

Correct Option: A

In the given circuit voltage across 18 Ω is 90 V: so, I across 18 Ω will be
I = 90 = 5 amp.
18

Voltage drop across AB = 5. 3 || 6 = 5 × 2 = 10 V
Voltage drop across AC = 90 + 10 = 100 V
Current in 5 Ω resistor = 100 = 20 amp.
5

so, Current flowing through 1 Ω resistor = 20 + 5 = 25 amp.
Voltage drop across 1 Ω = 25 × 1 = 25 V
so, voltage drop across the terminal E and F
= 25 + 100 = 125 V