Network Elements and the Concept of Circuit

Network Elements and the Concept of Circuit

Easy Questions

Network Theory

Network Elements and the Concept of Circuit
Network theory miscellaneous
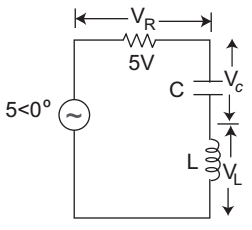
  1. In the circuit of the given figure, the magnitude of VL and VC are twice that of VR. The inductance of the coil is—










  1. View Hint View Answer Discuss in Forum

    It is given that VL = VC = 2VR means circuit in the resonance since here VL = VC
    VL = 2VR = 10
    ωL = 10


    L =
    10
    		 =
    10
    		= 31.8 mH
    2πφ2 × π × 50

    Correct Option: C

    It is given that VL = VC = 2VR means circuit in the resonance since here VL = VC
    VL = 2VR = 10
    ωL = 10


    L =
    10
    		 =
    10
    		= 31.8 mH
    2πφ2 × π × 50

  1. A voltage waveform V (t) = 12 t 2 is applied across 1 H inductor for t 0, with initial current through it being zero the current through the inductor for t 0 is given by—








  1. View Hint View Answer Discuss in Forum

    Current across inductor is given by the relation.

    i =
    1
    		 tV dt
    L0

    =
    1
    		 t12t 2 dt
    10

    = 12
    t3
    		= t3
    3

    Correct Option: D

    Current across inductor is given by the relation.

    i =
    1
    		 tV dt
    L0

    =
    1
    		 t12t 2 dt
    10

    = 12
    t3
    		= t3
    3

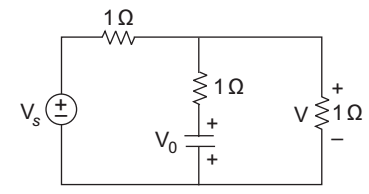
  1. Initial voltage on capacitor V0 as marked | V0 | = 5 V. Vs = 8 u(t), where u(t) is the unit step. The voltage marked V at t = 0+ is given by—










  1. View Hint View Answer Discuss in Forum

    If we consider the circuit carefully we see that there are two voltage source present in the circuit and if we have to calculate the net voltage in a particular resistance it can be easily calculated by using superposition theorem.
    Case I. When Vs = 8u (t) = 8 V source is treated, the equivalent circuit becomes.
    Apply voltage divides method, we get

    I =
    V
    		 =
    8
    8
    		 =
    16
    		 amp
    Req1 + 1 || 11 + (1 / 2)3


    I 1 = 16 3 × 1 2 = 8 3 amp
    Case II. When | V0 | = 5 V source is treated, the equivalent circuit becomes.
    I′ 2 =
    V
    		 =
    5

    Req1 + 1 || 1

    =
    5
    		 =
    10
    		amp.
    1 + (1 / 2)3


    I′ 1 = I′2 ×
    1
    		 =
    10
    		 x
    1

    1 + 132


    I′ 1 =
    5
    		amp.
    3

    The net current in 1 Ω resistance

    = I1 + I′ 1 =
    8
    		 +
    5
    		 =
    13
    		amp.
    333


    Voltage drop across 1 Ω =
    13
    		 x 1 =
    13
    		V
    33

    Correct Option: C

    If we consider the circuit carefully we see that there are two voltage source present in the circuit and if we have to calculate the net voltage in a particular resistance it can be easily calculated by using superposition theorem.
    Case I. When Vs = 8u (t) = 8 V source is treated, the equivalent circuit becomes.
    Apply voltage divides method, we get

    I =
    V
    		 =
    8
    8
    		 =
    16
    		 amp
    Req1 + 1 || 11 + (1 / 2)3


    I 1 = 16 3 × 1 2 = 8 3 amp
    Case II. When | V0 | = 5 V source is treated, the equivalent circuit becomes.
    I′ 2 =
    V
    		 =
    5

    Req1 + 1 || 1

    =
    5
    		 =
    10
    		amp.
    1 + (1 / 2)3


    I′ 1 = I′2 ×
    1
    		 =
    10
    		 x
    1

    1 + 132


    I′ 1 =
    5
    		amp.
    3

    The net current in 1 Ω resistance

    = I1 + I′ 1 =
    8
    		 +
    5
    		 =
    13
    		amp.
    333


    Voltage drop across 1 Ω =
    13
    		 x 1 =
    13
    		V
    33

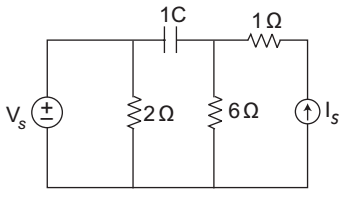
  1. The natural frequency of the circuit is given by—










  1. View Hint View Answer Discuss in Forum

    Redrawn circuit to calculate the natural frequency is given below.

    here natural frequency is given as Sn = – R eq . C.
    here R eq = 6, C = 1
    Sn = – 6 × 1 = – 6

    Correct Option: A

    Redrawn circuit to calculate the natural frequency is given below.

    here natural frequency is given as Sn = – R eq . C.
    here R eq = 6, C = 1
    Sn = – 6 × 1 = – 6

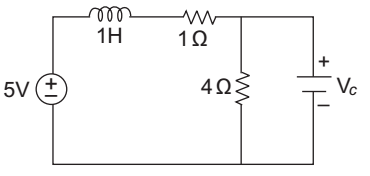
  1. Steady state is reached for the circuit. VC as marked in the circuit is—










  1. View Hint View Answer Discuss in Forum

    Redrawn circuit under steady state is given below.

    VC =
    4 × 5
    		= 4 V
    4 + 1

    Correct Option: B

    Redrawn circuit under steady state is given below.

    VC =
    4 × 5
    		= 4 V
    4 + 1