Network Elements and the Concept of Circuit Easy Questions and Answers | Page - 9

Network Elements and the Concept of Circuit

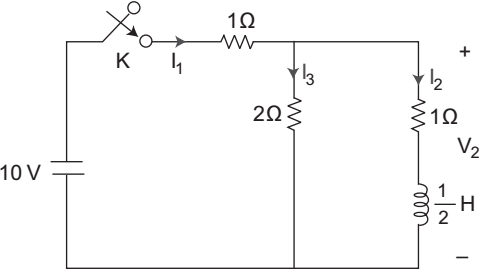
For fig. at time t ₀ after the switch K was closed, it is found that V₂ = + 5 V, determine the value of i ₂ (t ₀) and d / dt i₂ (t ₀)—

1. 2.5 amp, 5 amp/sec
1. 2.5 amp, 2.5 amp/sec
1. 5 amp, 2.5 amp/sec
1. 5 amp, 5 amp/sec

View Hint View Answer Discuss in Forum

Given V₂ = 5V
I ₁ = 10 – V₂ =
10 – 5 = 5
1 1

I ₃ = 5 = 2.5
2

I ₂ = I₁ – I₃ = 5 – 2.5 = 2.5 amp.
Voltage across 1 Ω resistance = 2.5 × 1 = 2.5 V
V_L = 5 – 2.5 = 2.5 V
Also, V_L = L di(t)
dt

2.5 = 1 / 2 di₂(t₀)
dt

or di₂(t₀) = 2.5 × 2 = 5 amp/sec
dt

Correct Option: A

Given V₂ = 5V
I ₁ = 10 – V₂ =
10 – 5 = 5
1 1

I ₃ = 5 = 2.5
2

I ₂ = I₁ – I₃ = 5 – 2.5 = 2.5 amp.
Voltage across 1 Ω resistance = 2.5 × 1 = 2.5 V
V_L = 5 – 2.5 = 2.5 V
Also, V_L = L di(t)
dt

2.5 = 1 / 2 di₂(t₀)
dt

or di₂(t₀) = 2.5 × 2 = 5 amp/sec
dt

Find the value of R so that V₂ = 2 volt—

1. 6 Ω
  5
1. 5 Ω
  6
1. 2 Ω
1. 5 Ω

View Hint View Answer Discuss in Forum

Given circuit

Apply KCL at node A
I ₁ + 4 = 2 I₁ + V₂
R

or 4 - 2 = I₁ (V2 = 2V)
R

4 – 2 =
8 = 5
R 5

∵ I₁ = 10 - 2 = 8
5 5

or 4R – 2 =
8
R 5

or 20 R – 10 = 8 R
or (20 – 8) R = 10
or 12 R = 10
or R = 10 =
5 Ω
12 6

Correct Option: B

Given circuit

Apply KCL at node A
I ₁ + 4 = 2 I₁ + V₂
R

or 4 - 2 = I₁ (V2 = 2V)
R

4 – 2 =
8 = 5
R 5

∵ I₁ = 10 - 2 = 8
5 5

or 4R – 2 =
8
R 5

or 20 R – 10 = 8 R
or (20 – 8) R = 10
or 12 R = 10
or R = 10 =
5 Ω
12 6

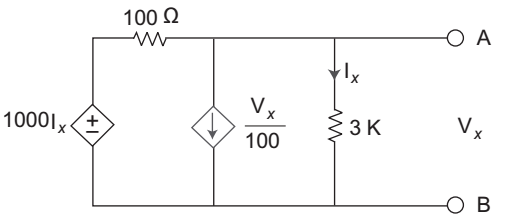
Find the Thevenin voltage and resistance for the given circuit shown below—

1. R_th = 58.82 Ω, V_th = 117.64 V
1. R_th = 117.64 Ω, V_th = 58.82 V
1. R_th = 58.82 Ω, V_th = 58.82 V
1. None of these

View Hint View Answer Discuss in Forum

Calculation for R_th
As there are many dependent sources are taking into account so in order to calculate the R_th let an imaginary current source say 2A is connected across the open terminal then R_th will be the ratio of
V_x =
V_x
I 2

On applying KCL at node N.
V_x - 1000 I_x +
V_x +
V_x = 2 ....(i)
100 100 3000

Also I_X = V_x = I₁....(ii)
3000

Solving equations (i) and (ii), we get
V_X = (58.82 × 2) V
so, R_th = V_x =
58.82 × 2 = 58.82 Ω
2 2

(∵ R_th = V_x = I₁, where I = 2 amp {imaginary source})
I

V_X = V_th = 58.82 × 2 = 117.6 V

Correct Option: A

Calculation for R_th
As there are many dependent sources are taking into account so in order to calculate the R_th let an imaginary current source say 2A is connected across the open terminal then R_th will be the ratio of
V_x =
V_x
I 2

On applying KCL at node N.
V_x - 1000 I_x +
V_x +
V_x = 2 ....(i)
100 100 3000

Also I_X = V_x = I₁....(ii)
3000

Solving equations (i) and (ii), we get
V_X = (58.82 × 2) V
so, R_th = V_x =
58.82 × 2 = 58.82 Ω
2 2

(∵ R_th = V_x = I₁, where I = 2 amp {imaginary source})
I

V_X = V_th = 58.82 × 2 = 117.6 V

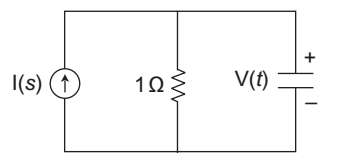
The initial voltage on the capacitor is V_c (0^–) = 2 V, I (s) = u (t) cos t find V (t) for t > 0—

1. V (t) = 1 cos (t – 45º) +
  3 e^{– t}
  2 2
1. V (t) = 2 cos (t – 45º) + 3 e^{+ t}
  2
1. V (t) = cos (t – 45º) + 1 e^{– 2t}
  2
1. V (t) = cos (t + 45º) + 3 e^{– 2t}
  2

View Hint View Answer Discuss in Forum

Here Z_eq = 1 .( 1 / Jω) , ω = 1 on comparing with I (s) = u (t) cos
1 + (1 / Jω)

or Z _eq = 1
1 + J

Since initial voltage on the capacitor is V(0^–) = 2 V,
so, V (t) J (s), Z_eq = cos t. 1 + A e^{– st}
1 + J

s= 1 cos (t– 45°) + A e^{– st} given that at t = 0. V (0) = 2 V
√2

so, 2 = 1 2 cos (0 – 45º) + A e^–5.0
√2

2 = 1 √2 + A
√2

or A = 3
2

S = 1 =
1 = 1
RC 1 x 1

V (t) = cos (t – 45°) + 3 e^{– t}
2

Correct Option: A

Here Z_eq = 1 .( 1 / Jω) , ω = 1 on comparing with I (s) = u (t) cos
1 + (1 / Jω)

or Z _eq = 1
1 + J

Since initial voltage on the capacitor is V(0^–) = 2 V,
so, V (t) J (s), Z_eq = cos t. 1 + A e^{– st}
1 + J

s= 1 cos (t– 45°) + A e^{– st} given that at t = 0. V (0) = 2 V
√2

so, 2 = 1 2 cos (0 – 45º) + A e^–5.0
√2

2 = 1 √2 + A
√2

or A = 3
2

S = 1 =
1 = 1
RC 1 x 1

V (t) = cos (t – 45°) + 3 e^{– t}
2

Direction: Fig. shows the statement for given question.

Current i at t = 0.5 sec will be—

1. 5 amp
1. 5 amp
  3
1. 3 amp
1. 3 amp
  5

View Hint View Answer Discuss in Forum

At t = 0.5 sec
30 u (t + 1) → exist and equal to 30 V
2 u (1 – t) → exist and equal to 2 amp.

Now, we will draw the equivalent circuit under this situation we get this situation is same as the above question so,
I = 5 amp.

Correct Option: A

At t = 0.5 sec
30 u (t + 1) → exist and equal to 30 V
2 u (1 – t) → exist and equal to 2 amp.

Now, we will draw the equivalent circuit under this situation we get this situation is same as the above question so,
I = 5 amp.