226. For the question 88, what will be the inverse z-transform for
     

     ROC	1	< |z| < 3
     	2

1. 1. 2	δ(n) +		1		n	u(– n – 1) –	1	(3)n u(n)
      3			2				3

   
   
   

   2. 2	δ(n) +		1		n	u(n) –	1	(3)n u(– n – 1)
      3			2				3

   
   
   

   3. 2	δ(n) +		1		n	u(n) –	1	(3)n u(n)
      3			2				3

   
   
   

   4. None of these

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Here, the ROC	1	< |z| < 3 is a ring,
   	2

   
   which means that the signal x(n) is two sided. Therefore, one of terms corresponds to a causal signal and the other is anti-causal signal.
   

   In the region	1	< |z| < 3
   	2

   
   

   i.e., |z| < 3 anti-causal and |z| >	1	causal,
   	2

   
   

   the pole p1 =	1	is interior and p2 = 3 is exterior and hence
   	2

   
   

   X(n) =	2	δ(n) +		1		n	u(n) –	1	(3)n u(– n – 1)
   	3			2				3

   
   Hence, alternative (B) is the correct answer.

   Correct Option: B

   Here, the ROC	1	< |z| < 3 is a ring,
   	2

   
   which means that the signal x(n) is two sided. Therefore, one of terms corresponds to a causal signal and the other is anti-causal signal.
   

   In the region	1	< |z| < 3
   	2

   
   

   i.e., |z| < 3 anti-causal and |z| >	1	causal,
   	2

   
   

   the pole p1 =	1	is interior and p2 = 3 is exterior and hence
   	2

   
   

   X(n) =	2	δ(n) +		1		n	u(n) –	1	(3)n u(– n – 1)
   	3			2				3

   
   Hence, alternative (B) is the correct answer.

---

227. The Z-transform of the signal x(n) = u(– n)

1. 1. 	1	, |Z| < 1
      	1 – Z

   
   
   

   2. 	1	, |Z| > 1
      	1 – Z

   
   
   

   3. 	Z	, |Z| > 1
      	Z – 1

   
   
   

   4. 	Z	, |Z| < 1
      	Z – 1

   
   
   

---

1. View Hint View Answer Discuss in Forum

   We know that
   

   u(n)←→	z	, ROC |z| > 1
   	z – 1

   
   By using time reversal property, we get
   

   u(n) ←→	z–1	or	1	or |z| < 1
   	z–1 – 1		1 – z

   
   ROC, |z^–1| > 1
   or |z|< 1
   Hence, alternative (A) is the correct choice.

   Correct Option: A

   We know that
   

   u(n)←→	z	, ROC |z| > 1
   	z – 1

   
   By using time reversal property, we get
   

   u(n) ←→	z–1	or	1	or |z| < 1
   	z–1 – 1		1 – z

   
   ROC, |z^–1| > 1
   or |z|< 1
   Hence, alternative (A) is the correct choice.

---

---

228. The ROC of the above question is given by—

1. 1. 	1	< |z| < 2
      	2

   
   
   

   2. 	1	< |z|
      	2

   
   
   

   3. |z| > 2

   
   
   

   4. None of these

   
   
   

---

1. View Hint View Answer Discuss in Forum

   ROC for x₁ (z): |z| < 2
   

   ROC for x2(z): |z| >	1
   	2

   
   

   ROC for x3(z): |z| >	1
   	3

   
   

   Hence, ROC for x(z):	1	< |z| < 2
   	2

   
   Hence, alternative (A) is the correct choice.

   Correct Option: A

   ROC for x₁ (z): |z| < 2
   

   ROC for x2(z): |z| >	1
   	2

   
   

   ROC for x3(z): |z| >	1
   	3

   
   

   Hence, ROC for x(z):	1	< |z| < 2
   	2

   
   Hence, alternative (A) is the correct choice.

---

229. For the given x(z) =	1
     	(1 + z– 1) (1 – z– 1)2

     the causal sequence x(n) will be—

1. 1. x(n) =		1	(1)n –	3	+	n		u(n)
      		4		4		2

   
   
   

   2. x(n) =		1	(– 1)n +	3	–	n		u(n)
      		4		4		2

   
   
   

   3. x(n) =		1	(– 1)n +	3	+	n		u(n)
      		4		4		2

   
   
   

   4. None of these

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Expanding the given X(z) in terms of the positive powers of z.
   

   x(z) =	1
   	(1 + z– 1) (1 – z– 1)2

   
   

   Hence, x(z) =	1
   	(z + 1) (z – 1)2

   
   

   Here, F(z) =	X(z)	=	z2
   	z		(z + 1) (z – 1)2

   
   

   =	A1	+	A2	+	A3
   	(z + 1)2		(z – 1)		(z – 1)2

   
   

   A1 = (z + 1) F(z)|z = – 1 =	z2	|z = – 1 =	1
   	(z – 1)2		4

   
   

   A2 =	d			z2
   	dz			z + 1		z = 1

   
   

   =	(z + 1) 2z – z2	|z = 1 =	3
   	(z + 1)2		4

   
   

   A3 = (z – 1)2 F(z)|z = 1 =	z2	|z = 1 =	1
   	(z + 1)		2

   
   

   Therefore, F(z) =	1	1	+	3	1	+	1	1
   	4	(z + 1)		4	(z – 1)		2	(z – 1)2

   
   

   =	1	z	+	3	z	+	1	z
   	4	(z + 1)		4	(z – 1)		2	(z – 1)2

   
   Taking inverse z-transform of x(z), we obtain
   

   x(n) =	1	(– 1)n u(n) +	3	u(n) +	1	nu(n)
   	4		4		2

   
   

   =		1	(– 1)n +	3	+	1	n		u(n)
   		4		4		2

   
   Hence alternative (C) is the correct choice.

   Correct Option: C

   Expanding the given X(z) in terms of the positive powers of z.
   

   x(z) =	1
   	(1 + z– 1) (1 – z– 1)2

   
   

   Hence, x(z) =	1
   	(z + 1) (z – 1)2

   
   

   Here, F(z) =	X(z)	=	z2
   	z		(z + 1) (z – 1)2

   
   

   =	A1	+	A2	+	A3
   	(z + 1)2		(z – 1)		(z – 1)2

   
   

   A1 = (z + 1) F(z)|z = – 1 =	z2	|z = – 1 =	1
   	(z – 1)2		4

   
   

   A2 =	d			z2
   	dz			z + 1		z = 1

   
   

   =	(z + 1) 2z – z2	|z = 1 =	3
   	(z + 1)2		4

   
   

   A3 = (z – 1)2 F(z)|z = 1 =	z2	|z = 1 =	1
   	(z + 1)		2

   
   

   Therefore, F(z) =	1	1	+	3	1	+	1	1
   	4	(z + 1)		4	(z – 1)		2	(z – 1)2

   
   

   =	1	z	+	3	z	+	1	z
   	4	(z + 1)		4	(z – 1)		2	(z – 1)2

   
   Taking inverse z-transform of x(z), we obtain
   

   x(n) =	1	(– 1)n u(n) +	3	u(n) +	1	nu(n)
   	4		4		2

   
   

   =		1	(– 1)n +	3	+	1	n		u(n)
   		4		4		2

   
   Hence alternative (C) is the correct choice.

---

---

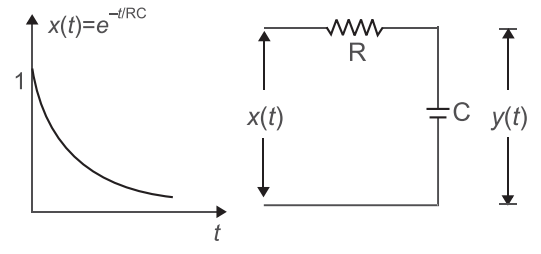
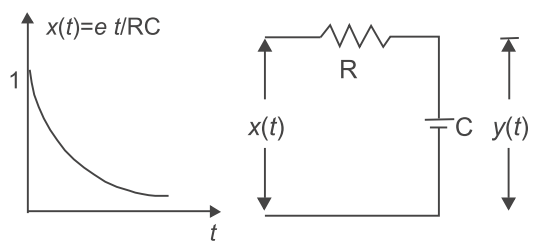
230. For the given system shown below. The output response of the low-pass RC network for are input signal x(t) = e^{– t/RC} will be—
     
     
     

1. 1. y(t) = RC t.e^{– t/RC}

   
   
   

   2. y(t) =	1	t.e– t/RC
      	RC

   
   
   

   3. y(t) = t.e^{– t/RC}

   
   
   

   4. None of these

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given that, x(t) = e^{– t/RC}
   

   X(s) =		z
   			s +	1
   				RC

   
   

   From figure Y(s) =	1		· X(s)
   	Cs
   	1	+ R
   	Cs

   
   

   or Y(s) =	1	·	1
   	1 + sRC					s +	1
   							RC

   
   

   or Y(s) =	RC
   	(1 + sRC)2

   
   

   or Y(s) =	·	1
   			(RC)2		s +	1		2
   						RC

   
   

   or Y(s) =	·	1							..........(A)
   			(RC)		s +	1		2
   						RC

   
   

   As we know that L[e– at] =	1
   	(s + a)2

   
   

   On putting a =	1	in equation (A)
   	RC

   
   

   we get, y(t) =	1	· t·e– t/RC
   	RC

   
   Hence, alternative (B) is the correct choice.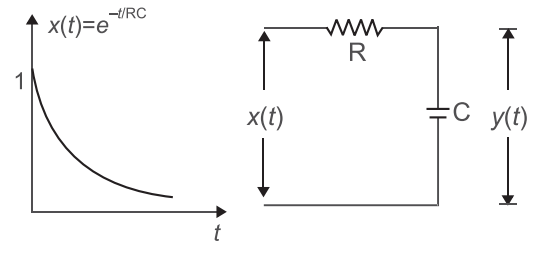

   
   

   Correct Option: B

   Given that, x(t) = e^{– t/RC}
   

   X(s) =		z
   			s +	1
   				RC

   
   

   From figure Y(s) =	1		· X(s)
   	Cs
   	1	+ R
   	Cs

   
   

   or Y(s) =	1	·	1
   	1 + sRC					s +	1
   							RC

   
   

   or Y(s) =	RC
   	(1 + sRC)2

   
   

   or Y(s) =	·	1
   			(RC)2		s +	1		2
   						RC

   
   

   or Y(s) =	·	1							..........(A)
   			(RC)		s +	1		2
   						RC

   
   

   As we know that L[e– at] =	1
   	(s + a)2

   
   

   On putting a =	1	in equation (A)
   	RC

   
   

   we get, y(t) =	1	· t·e– t/RC
   	RC

   
   Hence, alternative (B) is the correct choice.

   
   

---