-
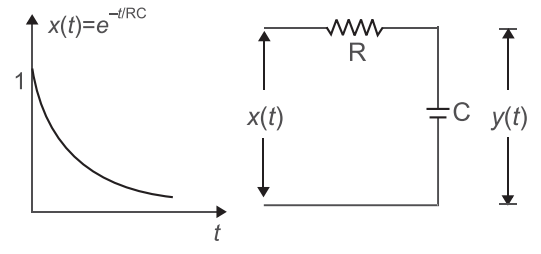
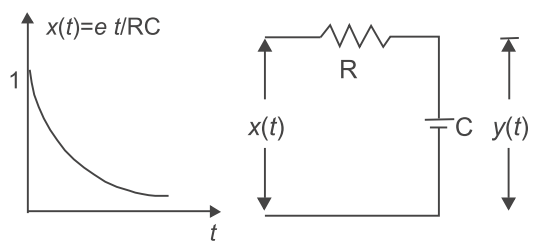
For the given system shown below. The output response of the low-pass RC network for are input signal x(t) = e– t/RC will be—
-
- y(t) = RC t.e– t/RC
-
y(t) = 1 t.e– t/RC RC - y(t) = t.e– t/RC
- None of these
Correct Option: B
Given that, x(t) = e– t/RC
| X(s) = |  |  | |||
| s + | |||||
| RC | |||||
| From figure Y(s) = | · X(s) | ||
| Cs | |||
| + R | |||
| Cs | |||
| or Y(s) = | · | 1 | |||||
| 1 + sRC |  | s + |  | ||||
| RC | |||||||
| or Y(s) = | (1 + sRC)2 |
| or Y(s) = | · | 1 | |||||||
| (RC)2 |  | s + |  | 2 | |||||
| RC | |||||||||
| or Y(s) = | · | 1 | ..........(A) | ||||||
| (RC) |  | s + |  | 2 | |||||
| RC | |||||||||
| As we know that L[e– at] = | (s + a)2 |
| On putting a = | in equation (A) | RC |
| we get, y(t) = | · t·e– t/RC | RC |
Hence, alternative (B) is the correct choice.