Signal and systems miscellaneous
- The Laplace transform of the function
f(t) = t sin at
-
View Hint View Answer Discuss in Forum
By using differentiation property
L{t sin at} = – d L {sin at} ds = – d 
a 
ds s2 + a2 = a 
– a · 2as 
(s2 + a2)2 = 2as (s2 + a2)2
Hence, alternative (A) is the correct choice.Correct Option: A
By using differentiation property
L{t sin at} = – d L {sin at} ds = – d 
a 
ds s2 + a2 = a 
– a · 2as 
(s2 + a2)2 = 2as (s2 + a2)2
Hence, alternative (A) is the correct choice.
- The Laplace transform of the function
f(t) = δ(t2 – 3t + 2)
-
View Hint View Answer Discuss in Forum
The given impulse function is
f(t) = δ(t2 – 3t2 + 2)
= δ[(t – 1) (t – 1)]
= δ(t – 1) u(t – 1) + δ(t – 2) u(t – 2)
Therefore, Laplace transform of
L{δ(t – 1)t + δ(t – 2)} = e– s + e– 2s
Hence, alternative (A) is the correct choice.Correct Option: A
The given impulse function is
f(t) = δ(t2 – 3t2 + 2)
= δ[(t – 1) (t – 1)]
= δ(t – 1) u(t – 1) + δ(t – 2) u(t – 2)
Therefore, Laplace transform of
L{δ(t – 1)t + δ(t – 2)} = e– s + e– 2s
Hence, alternative (A) is the correct choice.
- The Laplace transform of the function
f(t) = cos3 3t
-
View Hint View Answer Discuss in Forum
f(t) = cos3 3t
We know that
cos 3A = 4 cos3 A – 3 cos A
Therefore,L{cos3 3t} = 
cos 9t + 3 cos 3t 
4 = 1 
s + 3 s 
4 s2 + 92 s2 + 32 = 1 
s + 3s 
4 s2 + 18 s2 + 9 Correct Option: B
f(t) = cos3 3t
We know that
cos 3A = 4 cos3 A – 3 cos A
Therefore,L{cos3 3t} = 
cos 9t + 3 cos 3t 
4 = 1 
s + 3 s 
4 s2 + 92 s2 + 32 = 1 
s + 3s 
4 s2 + 18 s2 + 9
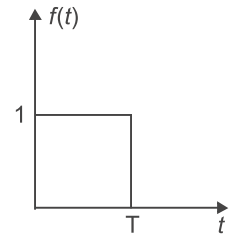
- The Laplace transform of the given figure will be—
-
View Hint View Answer Discuss in Forum
F(s) = L{f(t)} = ∫∞0 f(t)e– stdt
= ∫T0 1·e– st dt= 
e– st 
– T s 0 = 1 [e– sT – 1] s = 1 [1 – e– sT] s
Alternative method:
The given pulse is represented in terms of the step functions as
f(t) = u(t) – u(t – T)L{f(t)} = 1 – 1 e– st s s = 1 [1 – e– sT] s
Hence, alternative (C) is the correct choice.Correct Option: C
F(s) = L{f(t)} = ∫∞0 f(t)e– stdt

= ∫T0 1·e– st dt= 
e– st 
– T s 0 = 1 [e– sT – 1] s = 1 [1 – e– sT] s
Alternative method:
The given pulse is represented in terms of the step functions as
f(t) = u(t) – u(t – T)L{f(t)} = 1 – 1 e– st s s = 1 [1 – e– sT] s
Hence, alternative (C) is the correct choice.
- The Laplace transform of a single saw tooth pulse as shown in figure—

-
View Hint View Answer Discuss in Forum
L{f(t)} = ∞0 f(t)e– st dt
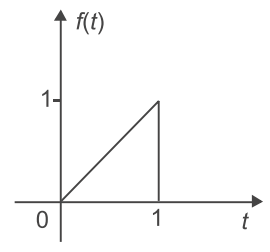
= ∫10 t e– st dt= 
t e– st – 1 e– st 
1 – s s2 0 = 

e– s – e– s 
– 
0 – 1 

– s s2 s2 = 1 – e– s 
1 + 1 
s2 s s2 Correct Option: C
L{f(t)} = ∞0 f(t)e– st dt

= ∫10 t e– st dt= 
t e– st – 1 e– st 
1 – s s2 0 = 

e– s – e– s 
– 
0 – 1 

– s s2 s2 = 1 – e– s 
1 + 1 
s2 s s2

