231. Let x[n] = anu[n] h[n] = bnu[n] What is the expression for y[n], for a discrete-time system?

1. 1. 	∞
      	∑	ak u[k]bn – k u[n – k]
      	k = – ∞

   
   
   

   2. 	∞
      	∑	an u[k]bn – k u[n – k]
      	k = – ∞

   
   
   

   3. 	∞
      	∑	ak u[n – k]bn u[k]
      	k = – ∞

   
   
   

   4. 	∞
      	∑	ak u[n – k]bn u[k]
      	k = – ∞

   
   
   

---

1. View Hint View Answer Discuss in Forum

   For any arbitrary signal x(n) the response of the system is given by
   

   	∞
   y(n) =	∑	x(k).x(n – k)
   	k = – ∞

   
   Here, x(n) = aⁿ.u(n)
   x(n) = bⁿ u(n)
   

   	∞
   So, y(n) =	∑	ak u(k).bn – k u[n – k]
   	k = – ∞

   
   Hence, alternative (A) is the correct answer.

   Correct Option: A

   For any arbitrary signal x(n) the response of the system is given by
   

   	∞
   y(n) =	∑	x(k).x(n – k)
   	k = – ∞

   
   Here, x(n) = aⁿ.u(n)
   x(n) = bⁿ u(n)
   

   	∞
   So, y(n) =	∑	ak u(k).bn – k u[n – k]
   	k = – ∞

   
   Hence, alternative (A) is the correct answer.

---

232. For the signal shown below—
     
     
     

1. 1. only Fourier transform exist

   
   
   

   2. only Laplace transform exists

   
   
   

   3. Both Laplace transform and Fourier transforms exist

   
   
   

   4. Neither Laplace transform nor Fourier transform exists

   
   
   

---

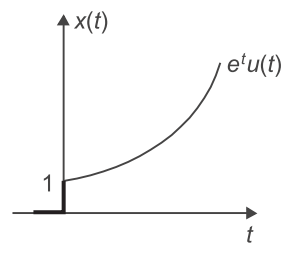
1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: B

   NA

---

---

233. The output y[n] of a discrete time LTI system is related to the input x(n) as given below:
     

     	∞
     y(n) =	∑	x(k)
     	k = 0

     
     Which one of the following correctly relates the z-transform of the input and output, denoted by x(z) and y(z), respectively?

1. 1. Y(z) = (1 – z^{– 1}) X(z)

   
   
   

   2. Y(z) = z^{– 1} X(z)

   
   
   

   3. Y(z) =	X(z)
      	1 – z– 1

   
   
   

   4. Y(z) =	dX (z)
      	dz

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given,
   

   	∞
   y(n) =	∑	x(k)
   	k = 0

   
   which represents an accumulator, whose z-transform is
   

   Y(z) =	z	· X(z)
   	z – 1

   
   

   or Y(z) =	X(z)
   	1 – z– 1

   
   Hence, alternative (C) is the correct choice.

   Correct Option: C

   Given,
   

   	∞
   y(n) =	∑	x(k)
   	k = 0

   
   which represents an accumulator, whose z-transform is
   

   Y(z) =	z	· X(z)
   	z – 1

   
   

   or Y(z) =	X(z)
   	1 – z– 1

   
   Hence, alternative (C) is the correct choice.

---

234. The Laplace transform of the function—
     f(t) = t³ + 3t² – 6t + 4

1. 1. 6	+	2	–	6	+	4
      s4		s3		s2		s

   
   
   

   2. 6	+	6	–	6	+	4
      s4		s3		s2		s

   
   
   

   3. 6	–	6	+	6	–	4
      s4		s3		s2		s

   
   
   

   4. 6	–	6	+	6	+	4
      s4		s3		s2		s

   
   
   

---

1. View Hint View Answer Discuss in Forum

   L{f(t)} = L{t³ + 3t² – 6t + 4}
   

   =	3!	+	3·2!	–	6·1!	+	4
   	s4		s3		s2		s

   
   

   =	3·2·1	+	3·2·1	–	6·1	+	4
   	s4		s3		s2		s

   
   

   =	6	+	6	–	6	+	4
   	s4		s3		s2		s

   
   Hence, alternative (B) is the correct answer.

   Correct Option: B

   L{f(t)} = L{t³ + 3t² – 6t + 4}
   

   =	3!	+	3·2!	–	6·1!	+	4
   	s4		s3		s2		s

   
   

   =	3·2·1	+	3·2·1	–	6·1	+	4
   	s4		s3		s2		s

   
   

   =	6	+	6	–	6	+	4
   	s4		s3		s2		s

   
   Hence, alternative (B) is the correct answer.

---

---

235. Which of the following is the inverse z-transform of
     

     X(z) =	z	|z| < 2
     	(z – 2) (z – 3)

1. 1. [2ⁿ – 3ⁿ] u(– n – 1)

   
   
   

   2. [3ⁿ – 2ⁿ] u(– n – 1)

   
   
   

   3. [2ⁿ – 3ⁿ] u(n + 1)

   
   
   

   4. [2ⁿ – 3ⁿ] u(n)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given that
   

   X(z) =	z	|z| < 2
   	(z – 2) (z – 3)

   
   

   or	X(z)	=	A	+	A
   	z		z – 2		z – 3

   
   

   or	X(z)	=	-1	+	1
   	z		z – 2		z – 3

   
   

   or X(z) = –		z		+		z
   		z – 2				z – 3

   
   

   or X(z) = –		1		+		1
   		1 – 2z– 1				1 – 3z– 1

   
   Now, since in the region |z| < 2 both the poles are exterior i.e., anti-causal and hence inverse z-transform.
   x(n) = [– (– 2ⁿ) + (– 3ⁿ)] u(– n – 1)
   or x(n) = (2ⁿ – 3ⁿ) u(– n – 1)
   Hence, alternative (A) is the correct choice.
   

   Correct Option: A

   Given that
   

   X(z) =	z	|z| < 2
   	(z – 2) (z – 3)

   
   

   or	X(z)	=	A	+	A
   	z		z – 2		z – 3

   
   

   or	X(z)	=	-1	+	1
   	z		z – 2		z – 3

   
   

   or X(z) = –		z		+		z
   		z – 2				z – 3

   
   

   or X(z) = –		1		+		1
   		1 – 2z– 1				1 – 3z– 1

   
   Now, since in the region |z| < 2 both the poles are exterior i.e., anti-causal and hence inverse z-transform.
   x(n) = [– (– 2ⁿ) + (– 3ⁿ)] u(– n – 1)
   or x(n) = (2ⁿ – 3ⁿ) u(– n – 1)
   Hence, alternative (A) is the correct choice.
   

---